题目内容
 在△ABC中,AB=AC,∠BAC=α,
在△ABC中,AB=AC,∠BAC=α,(1)直接写出∠ABC的大小(用含α的式子表示);
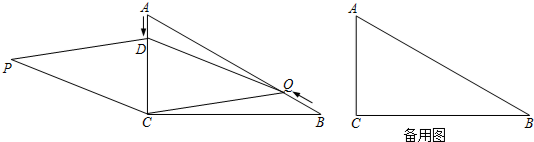
(2)当0°<α<60°时,将线段BC绕点B逆时针旋转60°得到线段BD,连接AD、CD.
①求证:△ABD≌△ACD;
②当α=40°,求∠ABD的度数.
考点:旋转的性质,全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)由等腰三角形的性质与三角形内角和定理可得∠ABC的大小;
(2)①由旋转的性质可得BC=BD,∠DBC=60°,所以△BCD为等边三角形,于是BD=CD,再根据SSS可得△ABD≌△ACD;
②先由(1)求得∠ABC=70°,再由△BCD为等边三角形可得∠BDC=60°,于是可得∠ABD的度数.
(2)①由旋转的性质可得BC=BD,∠DBC=60°,所以△BCD为等边三角形,于是BD=CD,再根据SSS可得△ABD≌△ACD;
②先由(1)求得∠ABC=70°,再由△BCD为等边三角形可得∠BDC=60°,于是可得∠ABD的度数.
解答:解:(1)∵AB=AC,
∴∠ABC=
(180°-∠BAC)=
×(180°-α)=90°-
α;
(2)①线段BC绕点B逆时针旋转60°得到线段BD,
则BC=BD,
∠DBC=60°
∴△BCD为等边三角形.
∴BD=CD
在△ABD和△ACD中,
,
∴△ABD≌△ACD (SSS);
②当α=40°时,
∠ABC=90°-
α=70°
∵△BCD为等边三角形.
∴∠BDC=60°,
∴∠ABD=∠ABC-∠BDC=10°.
∴∠ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)①线段BC绕点B逆时针旋转60°得到线段BD,
则BC=BD,
∠DBC=60°
∴△BCD为等边三角形.
∴BD=CD
在△ABD和△ACD中,
|
∴△ABD≌△ACD (SSS);
②当α=40°时,
∠ABC=90°-
| 1 |
| 2 |
∵△BCD为等边三角形.
∴∠BDC=60°,
∴∠ABD=∠ABC-∠BDC=10°.
点评:本题考查了全等三角形的判定与性质、等腰三角形的性质以及旋转的性质,综合性较强,熟练掌握定理及性质是解题的关键.

练习册系列答案
相关题目
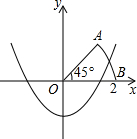 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有公共点,则实数k的取值范围是( )A、
| ||
B、-4≤k≤
| ||
C、C-4≤k≤
| ||
| D、-4≤k≤0 |
 如图,点P在反比例函数y=
如图,点P在反比例函数y=