题目内容
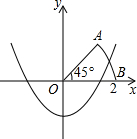 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有公共点,则实数k的取值范围是( )A、
| ||
B、-4≤k≤
| ||
C、C-4≤k≤
| ||
| D、-4≤k≤0 |
考点:二次函数的性质
专题:
分析:根据∠AOB=45°求出直线OA的解析式,然后与抛物线解析式联立求出有一个公共点时的k值,即为一个交点时的最大值,再求出抛物线经过点B时的k的值,即为一个交点时的最小值,然后写出k的取值范围即可.
解答:解:由图可知,∠AOB=45°,
∴直线OA的解析式为y=x,
联立
,
消掉y得,
x2-x+k=0,
△=b2-4ac=(-1)2-4×k=0,
即k=
时,抛物线与OA有一个交点,此交点的横坐标为
.
∵点B的坐标为(2,0),
∴OA=2,
∴点A的坐标为(
,
),
∴交点在线段AO上;
当抛物线经过点B(2,0)时,4+k=0,
解得k=-4,
∴抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是:-4≤k≤
.
故选:B.
∴直线OA的解析式为y=x,
联立
|
消掉y得,
x2-x+k=0,
△=b2-4ac=(-1)2-4×k=0,
即k=
| 1 |
| 4 |
| 1 |
| 2 |
∵点B的坐标为(2,0),
∴OA=2,
∴点A的坐标为(
| 2 |
| 2 |
∴交点在线段AO上;
当抛物线经过点B(2,0)时,4+k=0,
解得k=-4,
∴抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是:-4≤k≤
| 1 |
| 4 |
故选:B.
点评:本题考查了二次函数的性质,主要利用了联立两函数解析式确定交点个数的方法,根据图形求出有一个交点时的最大值与最小值是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有( )| A、6个 | B、5个 | C、4个 | D、3个 |
2008年5月12日四川汶川发生里氏8.0级大地震,国内外社会各界纷纷向灾区捐款捐物,抗震救灾,截至6月4日12时,全国共接收捐款约为43700000000元人民币.这笔款额用科学记数法表示正确的是( )
| A、0.437×1011 |
| B、4.4×1010 |
| C、4.37×1010 |
| D、43.7×109 |
关于正比例函数y=-2x,下列说法错误的是( )
| A、图象经过原点 |
| B、图象经过第二,四象限 |
| C、y随x增大而增大 |
| D、点(2,-4)在函数的图象上 |
三条线段长分别是
、
、
,则此三条线段所构成的三角形是( )
| 3 |
| 7 |
| 10 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、一般的不等边三角形 |
| D、直角三角形 |
下边给出的是2010年11月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是( )
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
| A、69 | B、54 | C、27 | D、40 |
下列命题的逆命题不正确的是( )
| A、同旁内角互补,两直线平行 |
| B、正方形的四个角都是直角 |
| C、若xy=0,则x=0 |
| D、平行四边形的对角线互相平分 |
 在△ABC中,AB=AC,∠BAC=α,
在△ABC中,AB=AC,∠BAC=α,