题目内容
8.在平面直角坐标系xOy中,直线y=kx+5(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为A,与x轴交于点B(5,0).(1)求k的值;
(2)若AB=3$\sqrt{2}$,求m的值.
分析 (1)将点B(5,0)代入直线y=kx+5中,得出关于k的一元一次方程,解方程即可得出结论;
(2)根据题意得知点A在第一象限或第四象限.过点A作AC⊥x轴于点C,分点A在第一第四象限考虑,得出A点的坐标,将A点的坐标代入双曲线y=$\frac{m}{x}$中,得出关于m的一元一次方程,解方程即可得出结论.
解答 解:(1)∵直线y=kx+5与x轴交于点B(5,0),
∴有0=5k+5,
解得:k=-1.
(2)由题意知,点A在第一象限或第四象限.
当点A在第一象限时,过点A作AC⊥x轴于点C,如图1所示.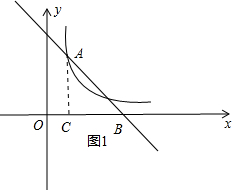
∵AB=3$\sqrt{2}$,∠ABC=45°,
∴AC=BC=3,
∴点A的坐标为(2,3).
将点A的坐标代入y=$\frac{m}{x}$中,有3=$\frac{m}{2}$,
解得:m=6.
当点A在第四象限时,过点A作AC⊥x轴于点C,如图2所示.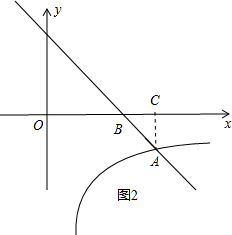
同理可得点A的坐标为(8,-3).
将点A的坐标代入y=$\frac{m}{x}$中,有-3=$\frac{m}{8}$,
解得:m=-24.
综上所述,m=6或m=-24.
点评 本题考查了反比例函数与一次函数的交点问题以及解一元一次方程,解题的关键是:(1)将点B的坐标代入直线解析式得出关于k的一元一次方程;(2)将点A的坐标代入双曲线解析式得出关于k的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,将点的坐标代入函数解析式中得出关于未知数的方程是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
3.长城、故宫等是我国第一批成功入选世界遗产的文化古迹,长城总长约6700 000米.将6700 000用科学记数法表示应为( )
| A. | 67×106 | B. | 6.7×106 | C. | 6.7×106 | D. | 0.67×106 |
18.据北京市商务委表示,除夕至初五,21家节能减排补贴商品定点销售企业销售额超过28000000元.将28000000用科学记数法表示应为( )
| A. | 0.28×108 | B. | 2.8×108 | C. | 2.8×107 | D. | 28×106 |
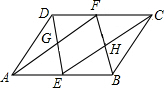 如图,在?ABCD中,E,F分别是AB,CD的中点,连结DE,AF,CF,BF,分别相交于点G,H.试说明四边形EHFG是平行四边形.
如图,在?ABCD中,E,F分别是AB,CD的中点,连结DE,AF,CF,BF,分别相交于点G,H.试说明四边形EHFG是平行四边形.