题目内容
20.计算:$\frac{1}{3+\sqrt{3}}$+$\frac{1}{5\sqrt{3}+3\sqrt{5}}$+$\frac{1}{7\sqrt{5}+5\sqrt{7}}$+…+$\frac{1}{121\sqrt{119}+119\sqrt{121}}$的值.分析 根据每个加数的特点,推出一般规律为$\frac{1}{(2n+1)\sqrt{2n-1}+(2n-1)\sqrt{2n+1}}$═$\frac{1}{2}$($\frac{1}{\sqrt{2n-1}}$-$\frac{1}{\sqrt{2n+1}}$),将所得式子化简,分别取n=1,2,3,…,60,寻找抵消规律,得出结论.
解答 解:∵$\frac{1}{(2n+1)\sqrt{2n-1}+(2n-1)\sqrt{2n+1}}$
=$\frac{1}{2}$[$\frac{(2n+1)-(2n-1)}{(2n+1)\sqrt{2n-1}+(2n-1)\sqrt{2n+1}}$
=$\frac{1}{2}$[$\frac{(\sqrt{2n+1})^{2}-(\sqrt{2n-1})^{2}}{\sqrt{2n+1}×\sqrt{2n-1}(\sqrt{2n+1}+\sqrt{2n-1})}$
=$\frac{1}{2}$$\frac{\sqrt{2n+1}-\sqrt{2n-1}}{\sqrt{2n+1}×\sqrt{2n-1}}$
=$\frac{1}{2}$($\frac{1}{\sqrt{2n-1}}$-$\frac{1}{\sqrt{2n+1}}$)
∴分别取n=1,2,3,…60得
原式=$\frac{1}{2}$[(1-$\frac{1}{\sqrt{3}}$)+($\frac{1}{\sqrt{3}}$-$\frac{1}{\sqrt{5}}$)+($\frac{1}{\sqrt{5}}$-$\frac{1}{\sqrt{7}}$)+…+($\frac{1}{\sqrt{119}}$-$\frac{1}{\sqrt{121}}$)
=$\frac{1}{2}$(1-$\frac{1}{11}$)
=$\frac{5}{11}$.
点评 本题考查了二次根式的化简求值,观察式子的特点,得出一般规律,将一般规律化简代值,再观察抵消规律是解题的关键.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 和为180°的两个角是邻补角 | |
| B. | 一条直线的垂线有且只有一条 | |
| C. | 点到直线的距离是指这点到直线的垂线段 | |
| D. | 两条直线被第三条直线所截,如内错角相等,则同位角必相等 |
 如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.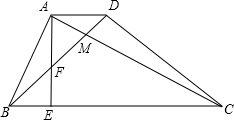 如图:四边形ABCD中,AB=AD,对角线AC,BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD于点F.
如图:四边形ABCD中,AB=AD,对角线AC,BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD于点F.