题目内容
17.解方程组(1)$\left\{\begin{array}{l}{x-2y=z}\\{3x+2y=1}\\{2x-y=z+\frac{1}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+2y+5z=2}\\{x-2y-z=6}\\{4x+2y-7z=30}\end{array}\right.$.
分析 (1)把①代入③得出2x+2y=1④,由②和④组成方程组,求出方程组的解,把x和y的值代入①求出z即可;
(2)①+②得出x+z=2④,②+③得出5x-8z=36⑤,由④和⑤组成方程组,求出方程组的解,把x和z的值代入②求出y即可.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=z①}\\{3x+2y=1②}\\{2x-y=z+\frac{1}{2}③}\end{array}\right.$
把①代入③得:2x-y=x-2y+$\frac{1}{2}$,
即2x+2y=1④,
由②和④组成方程组$\left\{\begin{array}{l}{2x+2y=1}\\{3x+2y=1}\end{array}\right.$,
解得:x=0,y=$\frac{1}{2}$,
把x=0,y=$\frac{1}{2}$代入①得:z=-1,
所以原方程组的解为:$\left\{\begin{array}{l}{x=0}\\{y=\frac{1}{2}}\\{z=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+2y+5z=2①}\\{x-2y-z=6②}\\{4x+2y-7z=30③}\end{array}\right.$
①+②得:4x+4z=8,
即x+z=2④,
②+③得:5x-8z=36⑤,
由④和⑤组成方程组$\left\{\begin{array}{l}{x+z=2}\\{5x-8z=36}\end{array}\right.$,
解得:x=4,z=-2,
把x=4,z=-2代入②得:4-2y+2=6,
解得:y=0,
所以原方程组的解为:$\left\{\begin{array}{l}{x=4}\\{y=0}\\{z=-2}\end{array}\right.$.
点评 本题考查了解三元一次方程组的应用,能把三元一次方程组转化成二元一次方程组是解此题的关键.

| 通话时长(x分钟) | 0<x≤4 | 4<x≤8 | 8<x≤12 | 12<x≤16 | 16<x≤20 |
| 频数(通话次数) | 28 | 14 | 6 | 16 | 10 |
(2)求通话时间不超过12分钟的频数和频率?
| A. | 和为180°的两个角是邻补角 | |
| B. | 一条直线的垂线有且只有一条 | |
| C. | 点到直线的距离是指这点到直线的垂线段 | |
| D. | 两条直线被第三条直线所截,如内错角相等,则同位角必相等 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
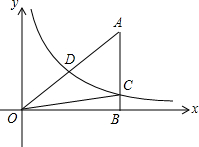 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上,若△OAC的面积为5,OA:OD=2:1,则k的值为8.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上,若△OAC的面积为5,OA:OD=2:1,则k的值为8.