题目内容
8．
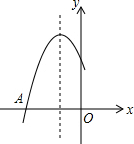如图是二次函数y=ax2+bx+c过点A（-3，0），对称轴为x=-1．给出四个结论：①b2＞4ac，②2a+b=0；③a-b+c=0；④5a＜b．其中正确结论是（ ）| A． | ②④ | B． | ①④ | C． | ②③ | D． | ①③ |
分析 ①正确．根据抛物线与x轴有两个交点即可判定．
②错误．根据对称轴x=-1即可判定．
③错误．根据x=-1时，y＞0即可判定．
④正确．由b=2a，a＜0，即可判定5a＜2a由此即可解决问题．
解答 解：∵抛物线与x轴有两个交点，
∴△＞0，即b2-4ac＞0，
∴b2＞4ac，故①正确．
∵对称轴x=-1，
∴-$\frac{b}{2a}$=-1，
∴b=2a，
∴2a-b=0，故②错误，
∵x=-1时，y＞0，
∴a-b+c＞0，故③错误，
∵b=2a，a＜O，
∴5a＜2a，即5a＜b，故④正确，
故选B．
点评 本题考查二次函数的图象与系数的关系、解题的关键是熟练掌握基本知识，读懂图象信息，充分利用图象信息解决问题，属于中考常考题型．
练习册系列答案
相关题目
19．
如图，直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E和B、D、F，若AC=4，AE=10，BF=$\frac{15}{2}$，则DF的长为（ ）
如图，直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E和B、D、F，若AC=4，AE=10，BF=$\frac{15}{2}$，则DF的长为（ ）| A． | $\frac{9}{2}$ | B． | 10 | C． | 3 | D． | $\frac{7}{2}$ |
3．下列各数中，比1大的数是（ ）
| A． | 0 | B． | -|-2| | C． | $\sqrt{2}$ | D． | -3 |
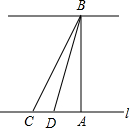某市为了改善市区交通状况，计划修建一座新大桥，如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直与新大桥AB的直线型道路l上测得如下数据：∠BDA=76.1°，∠BCA=68.2°，CD=82米．求AB的长（精确到0.1米，sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.0；sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.5．）
20．已知命题：等边三角形是等腰三角形．则下列说法正确的是（ ）
| A． | 该命题为假命题 | B． | 该命题为真命题 | ||
| C． | 该命题的逆命题为真命题 | D． | 该命题没有逆命题 |