题目内容
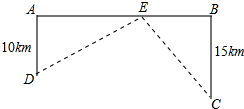如图，铁路上A、B两点相距25km，C、D为两个村庄，DA⊥AB于点A，CB⊥AB于点B，且DA=10km，CB=15km，现要在AB之间建一个货物中转站E，使得C、D两村到中转站E的距离相等，而且要求DE⊥CE，则中转站E应建在距离点B考点：勾股定理的应用
专题：
分析：利用DE=CE，再结合勾股定理求出即可．
解答：解：设AE=xkm，则BE=（25-x）km，根据题意可得：
∵DE=CE，
∴AD2+AE2=BE2+BC2，
故102+x2=（25-x）2+152，
解得：x=15，
∴BE=25-15=10．
故答案为：10．
∵DE=CE，
∴AD2+AE2=BE2+BC2，
故102+x2=（25-x）2+152，
解得：x=15，
∴BE=25-15=10．
故答案为：10．
点评：此题主要考查了勾股定理的应用，利用DE=CE得出是解题关键．
练习册系列答案
相关题目
用6个小立方块搭一个几何体，它的从正面看和从上面看的形状图如图所示，尝试画出所有可能的从左面看的形状图．在平面直角坐标系中，将抛物线y=x2+3x+m向右平移5个单位，则平移前后两条抛物线关于某直线对称，这条直线是（ ）
A、直线x=
| ||
| B、直线x=1 | ||
| C、直线x=2 | ||
D、直线x=
|
如图，∠A=∠B，CE∥AD，交AB于点E，CE=10cm，求BC的长度．
如图，△ABC中，E、F分别是AB、AC的点，AD平分∠BAC，DE⊥AB，DF⊥AC．求证：AD⊥EF．
如图，直线a∥b，三角形的直角顶点在直线a上，已知∠1=35°，则∠2的度数是（ ）| A、25° | B、55° |
| C、65° | D、155° |