题目内容
 如图,△ABC中,E、F分别是AB、AC的点,AD平分∠BAC,DE⊥AB,DF⊥AC.求证:AD⊥EF.
如图,△ABC中,E、F分别是AB、AC的点,AD平分∠BAC,DE⊥AB,DF⊥AC.求证:AD⊥EF.考点:角平分线的性质,全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:易证△AED≌△AFD,得AE=AF,利用等腰三角形三线合一可得证结论.
解答:证明:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF.
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,
在△AED和△AFD中,
|
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF.
点评:本题主要考查全等三角形的判定和性质及等腰三角形的判定和性质,掌握全等三角形的对应边相等及等腰三角形“三线合一”的性质是解题的关键.

练习册系列答案
相关题目
下列说法:①平角就是一条直线;②直线比射线线长;③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个;④连接两点的线段叫两点之间的距离;⑤两条射线组成的图形叫做角;⑥一条射线把一个角分成两个角,这条射线是这个角的角平分线,其中正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
从一副扑克牌中任意抽取一张,正好为K的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在如图所示的世界人口扇形统计图中,印度人口占世界人口的
在如图所示的世界人口扇形统计图中,印度人口占世界人口的 如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么?
如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么?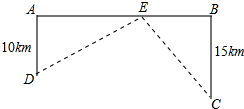 如图,铁路上A、B两点相距25km,C、D为两个村庄,DA⊥AB于点A,CB⊥AB于点B,且DA=10km,CB=15km,现要在AB之间建一个货物中转站E,使得C、D两村到中转站E的距离相等,而且要求DE⊥CE,则中转站E应建在距离点B
如图,铁路上A、B两点相距25km,C、D为两个村庄,DA⊥AB于点A,CB⊥AB于点B,且DA=10km,CB=15km,现要在AB之间建一个货物中转站E,使得C、D两村到中转站E的距离相等,而且要求DE⊥CE,则中转站E应建在距离点B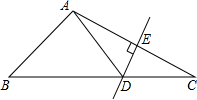 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是 如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=75°,∠AED=50°,求∠BDF的度数.
如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=75°,∠AED=50°,求∠BDF的度数.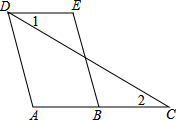 如图,AD∥BE,∠1=∠2,∠A=105°,求∠E的度数.
如图,AD∥BE,∠1=∠2,∠A=105°,求∠E的度数.