题目内容
在平面直角坐标系中,将抛物线y=x2+3x+m向右平移5个单位,则平移前后两条抛物线关于某直线对称,这条直线是( )
A、直线x=
| ||
| B、直线x=1 | ||
| C、直线x=2 | ||
D、直线x=
|
考点:二次函数图象与几何变换
专题:
分析:先把y=x2+3x+配成顶点式,得到抛物线y=x2+3x+的顶点坐标为(-
,m-
),再根据点平移的规律得到点(-
,m-
)向右平移5个单位的对应点的坐标为(
,m-
),然后通过确定两顶点关于直线x=1对称得到两抛物线关于此直线对称.
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 7 |
| 2 |
| 9 |
| 4 |
解答:解:∵y=x2+3x+m=(x+
)2+m-
,
∴抛物线y=x2+3x+m的顶点坐标为(-
,m-
),
∵点(-
,m-
)向右平移5个单位得到对应点的坐标为(
,m-
),
∴平移后得抛物线解析式为y=(x-
)2+m-
,
∵点(-
,m-
)与点(
,m-
)关于直线x=1对称,
∴平移前后两条抛物线关于直线x=1对称.
故选B.
| 3 |
| 2 |
| 9 |
| 4 |
∴抛物线y=x2+3x+m的顶点坐标为(-
| 3 |
| 2 |
| 9 |
| 4 |
∵点(-
| 3 |
| 2 |
| 9 |
| 4 |
| 7 |
| 2 |
| 9 |
| 4 |
∴平移后得抛物线解析式为y=(x-
| 7 |
| 2 |
| 9 |
| 4 |
∵点(-
| 3 |
| 2 |
| 9 |
| 4 |
| 7 |
| 2 |
| 9 |
| 4 |
∴平移前后两条抛物线关于直线x=1对称.
故选B.
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
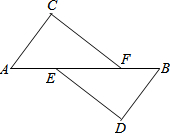 已知,如图:A、E、F、B在一条直线上,AC=BD,∠C=∠D,CF∥DE.
已知,如图:A、E、F、B在一条直线上,AC=BD,∠C=∠D,CF∥DE.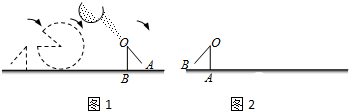
 如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么?
如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么? 如图,△ABC的面积等于25cm2,AE=ED,BD=3DC,则图中阴影部分的面积等于
如图,△ABC的面积等于25cm2,AE=ED,BD=3DC,则图中阴影部分的面积等于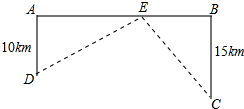 如图,铁路上A、B两点相距25km,C、D为两个村庄,DA⊥AB于点A,CB⊥AB于点B,且DA=10km,CB=15km,现要在AB之间建一个货物中转站E,使得C、D两村到中转站E的距离相等,而且要求DE⊥CE,则中转站E应建在距离点B
如图,铁路上A、B两点相距25km,C、D为两个村庄,DA⊥AB于点A,CB⊥AB于点B,且DA=10km,CB=15km,现要在AB之间建一个货物中转站E,使得C、D两村到中转站E的距离相等,而且要求DE⊥CE,则中转站E应建在距离点B 如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=75°,∠AED=50°,求∠BDF的度数.
如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=75°,∠AED=50°,求∠BDF的度数.