题目内容
 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC=30°,AD=3,BD=5.求四边形ABCD的面积.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC=30°,AD=3,BD=5.求四边形ABCD的面积.考点:正弦定理与余弦定理
专题:
分析:首先作点A关于CD的对称点E,进而得出△ADE为等边三角形,再证明△BAE≌△CAD(SAS),再利用余弦定理得出AB2的值,进而得出S四边形ABCD=S△ABC+S△ACD=S△ABC+
S四边形ACED求出即可.
| 1 |
| 2 |
解答: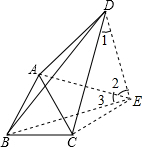 解:作点A关于CD的对称点E,连接DE,CE,BE,
解:作点A关于CD的对称点E,连接DE,CE,BE,
则有AD=ED=3,∠1=∠ADC=30°,
故∠ADE=2∠ADC=60°,
则△ADE为等边三角形,
故AE=DE=AD=3,∠DAE=∠2=60°,CD⊥AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=60°+∠CAE=∠DAE+∠CAE=∠CAD,
在△BAE和△CAD中
∵
,
∴△BAE≌△CAD(SAS),
∴∠3=∠ADC=30°,BE=CD,
∴∠BED=∠3+∠2=30°+60°=90°,
∴CD=BE=
=
=4,
在△AEB中,由余弦定理,则:
AB2=AE2+BE2-2×AE×BE×cos∠3
=32+42-2×3×4×cos30°
=25-12
,
则S四边形ABCD=S△ABC+S△ACD=S△ABC+
S四边形ACED
=
×AB×AC×sin∠BAC+
×
×AE×CD
=
(25-12
)×sin60°+
×
×3×4
=
-6.
 解:作点A关于CD的对称点E,连接DE,CE,BE,
解:作点A关于CD的对称点E,连接DE,CE,BE,则有AD=ED=3,∠1=∠ADC=30°,
故∠ADE=2∠ADC=60°,
则△ADE为等边三角形,
故AE=DE=AD=3,∠DAE=∠2=60°,CD⊥AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=60°+∠CAE=∠DAE+∠CAE=∠CAD,
在△BAE和△CAD中
∵
|
∴△BAE≌△CAD(SAS),
∴∠3=∠ADC=30°,BE=CD,
∴∠BED=∠3+∠2=30°+60°=90°,
∴CD=BE=
| BD2-DE2 |
| 52-32 |
在△AEB中,由余弦定理,则:
AB2=AE2+BE2-2×AE×BE×cos∠3
=32+42-2×3×4×cos30°
=25-12
| 3 |
则S四边形ABCD=S△ABC+S△ACD=S△ABC+
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
25
| ||
| 4 |
点评:此题主要考查了余弦定理和全等三角形的判定与性质以及等边三角形的判定与性质等知识,得出AB2的值是解题关键.

练习册系列答案
相关题目
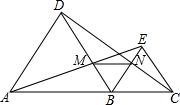 如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,求证:
如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,求证: 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则CD为
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则CD为