题目内容
14.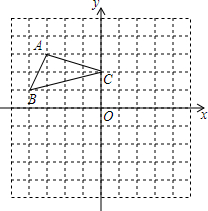 方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A1B1C1.
(2)求点B在旋转过程中所经过的路径长(结果保留π)
分析 (1)根据旋转的性质即可得到图形,
(2)得出旋转后的△A1B1C1,再利用弧长公式求出点B所经过的路径长.
解答  解(1)如图所示,图略,能正确画出图形给此题主要考查了弧长公式的应用以及图形的旋转与平移变换,根据已知得出对应点位置是解题关键.
解(1)如图所示,图略,能正确画出图形给此题主要考查了弧长公式的应用以及图形的旋转与平移变换,根据已知得出对应点位置是解题关键.
(2)∵BO=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴点B在旋转过程中所经过的路径长为$\frac{90π•\sqrt{17}}{180}$=$\frac{\sqrt{17}}{2}$π.
点评 此题主要考查了弧长公式的应用以及图形的旋转与平移变换,根据已知得出对应点位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{121}$=±11 | B. | ±$\sqrt{\frac{9}{25}}$=$\frac{3}{5}$ | C. | $\sqrt{(-\frac{1}{3})^{2}}$=-$\frac{1}{3}$ | D. | $\sqrt{0.16}$=0.4 |

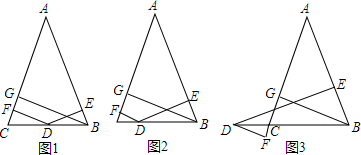
 如图所示,OB为正北方向,直线AD,BG,FC相交于点O,且AD与BG相互垂直,OE为南偏东25°的射线,且OE平分∠FOD,求∠COB的度数.
如图所示,OB为正北方向,直线AD,BG,FC相交于点O,且AD与BG相互垂直,OE为南偏东25°的射线,且OE平分∠FOD,求∠COB的度数. 如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°, 在平面直角坐标系xOy中,顶点D在第一象限的抛物线y=-x2-kx-(k-1)与x轴交于A(x1,0)、B(x2,0)两点(点A在点B的左侧,OA<OB),交y 轴于点C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.
在平面直角坐标系xOy中,顶点D在第一象限的抛物线y=-x2-kx-(k-1)与x轴交于A(x1,0)、B(x2,0)两点(点A在点B的左侧,OA<OB),交y 轴于点C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.