题目内容
12.下列说法正确的个数是( )①若mx=nx,则m=n;
②若△ABC中,sinA=$\frac{1}{2}$,则∠A=30°;
③一个角的两边分别垂直于另一个角的两边,则这两个角相等;
④等腰三角形的高、中线、角平分线互相重合;
⑤分式方程$\frac{3}{{x}^{2}-x}$$+\frac{6}{1-{x}^{2}}$=$\frac{7}{{x}^{2}+x}$的增根是0和1、-1;
⑥若n可以取从1到2016之间的正整数(包括1与2016),则二次函数y=(n2+n)x2-(2n+1)x+1的图象在x轴上所截得的线段之和为$\frac{2016}{2017}$.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 把错误的命题举出反例或者说出原因,正确的命题进行说明或推导,从而可以解答本题.
解答 解:∵若x=0时,则mx=nx,此时m、n可以为任意数,故①错误;
∵sin30°=$\frac{1}{2}$,在△ABC中,sinA=$\frac{1}{2}$,∴∠A=30°,故②正确;
∵四边形内角和等于360°,∴一个角的两边分别垂直于另一个角的两边,则这两个角互补,故③错误;
等腰三角形底边上的高、中线、角平分线互相重合,腰上的高、中线、角平分线不一定重合,故④错误;
分式方程$\frac{3}{{x}^{2}-x}$$+\frac{6}{1-{x}^{2}}$=$\frac{7}{{x}^{2}+x}$如果有增根,则x(x-1)(x+1)=0,得x=0或x=1或x=-1,故⑤正确;
∵(n2+n)x2-(2n+1)x+1=0,
解得,x=$\frac{1}{n}$或x=$\frac{1}{n+1}$,
∴二次函数y=(n2+n)x2-(2n+1)x+1的图象在x轴上所截得的线段长为:$\frac{1}{n}-\frac{1}{n+1}$=$\frac{1}{n(n+1)}$,
∴若n可以取从1到2016之间的正整数(包括1与2016),则二次函数y=(n2+n)x2-(2n+1)x+1的图象在x轴上所截得的线段之和为:
$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$
=$\frac{2016}{2017}$,
故⑥正确;
故选D.
点评 本题考查命题与定理,解题的关键是明确题意,可以对错误的命题举出反例或说明原因,正确的命题进行说明或推导.

 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )| A. | b-a>0 | B. | -a<0 | C. | |a|<|b| | D. | ab<0 |
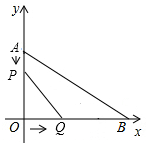 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.