方程与化简(1)$\frac{5x-4}{x-2}=\frac{4x+10}{3x-6}-1$(2)$\frac{x-3}{x-2}+1=\frac{3}{2-x}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．方程与化简
（1）$\frac{5x-4}{x-2}=\frac{4x+10}{3x-6}-1$
（2）$\frac{x-3}{x-2}+1=\frac{3}{2-x}$．

分析分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答解：（1）去分母得，
3（5x-4）=4x+10-（3x-6）
解得：x=2
经检验：x=2不是原方程的解，
∴原方程无解．
（2）去分母得，
x-3+x-2=-3
解得：x=1
经检验：x=1是原分式方程的解．

点评此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

练习册系列答案

相关题目

7．一元二次方程x²-4=0的根为（　　）

x₁=2，x₂=-2

8．为了解某类烟花爆竹燃放安全情况，宜采用抽样调查（填“全面调查”或“抽样调查”）的方式进行调查．

5．计算：
（1）$\sqrt{32}$-5$\sqrt{\frac{1}{2}}$+6$\sqrt{\frac{1}{8}}$；
（2）$（{\sqrt{3}+\sqrt{2}+\sqrt{5}}）（{\sqrt{3}-\sqrt{2}-\sqrt{5}}）$．

12．

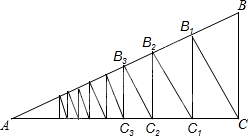如图，在Rt△ABC中，BC⊥AC，∠BAC=30°，CB₁⊥AB，B₁C₁⊥AC，C₁B₂⊥AB，B₂C₂⊥AC…以此类推，若BC=a，则B_nC_n=（$\frac{3}{4}$）ⁿa．

2．若|a-1|+|b+2|=0，求|a+b|的值．

6．

如图，不等长的两条对角线AC、BD相交于点O，且将四边形ABCD分成甲、乙、丙、丁四个三角形．若OA：OC=OB：OD=1：2，则甲、乙、丙、丁这4个三角形中，一定相似的有甲丙．

7．把抛物线y=-2x²的图象向左平移4个单位，再向上平移3个单位，所得的图象的表达式（　　）

试题分类