题目内容
5.计算:(1)$\sqrt{32}$-5$\sqrt{\frac{1}{2}}$+6$\sqrt{\frac{1}{8}}$;
(2)$({\sqrt{3}+\sqrt{2}+\sqrt{5}})({\sqrt{3}-\sqrt{2}-\sqrt{5}})$.
分析 (1)首先化简二次根式,然后合并同类二次根式即可;
(2)首先利用平方差公式计算,然后用完全平方公式计算即可.
解答 解:(1)原式=4$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$+$\frac{3\sqrt{2}}{2}$=3$\sqrt{2}$;
(2)原式=($\sqrt{3}$)2-($\sqrt{2}$+$\sqrt{5}$)2=3-(2+5+2$\sqrt{10}$)=3-7-2$\sqrt{10}$=-4-2$\sqrt{10}$.
点评 本题考查了二次根式的混合运算,正确理解乘法公式是解决本题的关键.

练习册系列答案
相关题目
10.在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
这此测试成绩的中位数和众数分别为( )
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 1 | 4 | 2 | 5 | 2 |
| A. | 47,49 | B. | 47,50 | C. | 48,49 | D. | 48,50 |
14.下列各式中属于最简二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{{x}^{2}{y}^{3}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{2}}$ |
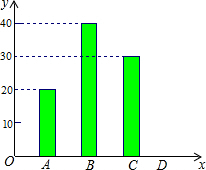 “五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
“五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题: 如图:一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1、n)两点.
如图:一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1、n)两点. 如图,矩形OABC的两边OA,OC在坐标轴上,且OC=2OA,M,N分别为OA,OC的中点,BM与AN交于点E,且四边形EMON的面积为2,
如图,矩形OABC的两边OA,OC在坐标轴上,且OC=2OA,M,N分别为OA,OC的中点,BM与AN交于点E,且四边形EMON的面积为2,