题目内容
1. 已知△ABC中,AD是高,E,F,G为中点,求证:四边形DEFG是等腰梯形.
已知△ABC中,AD是高,E,F,G为中点,求证:四边形DEFG是等腰梯形.
分析 由E,F,G分别是BC,AC,BA的中点,根据三角形的中位线的性质,可得GF∥BC,EF=$\frac{1}{2}$AB,又由AD⊥BC,利用直角三角形斜边中线的性质,可得DG=$\frac{1}{2}$AB,即可得DG=EF,证得四边形DEFG是等腰梯形.
解答 证明:∵E,F,G分别是BC,AC,BA的中点,
∴GF∥BC,EF=$\frac{1}{2}$AB,
∵GF≠DE,
∴四边形DEFG是梯形,
∵AD⊥BC,
即∠ADB=90°,
∵G是AB的中点,
∴DG=$\frac{1}{2}$AB,
∴DG=EF,
∴四边形DEFG是等腰梯形.
点评 此题考查了等腰梯形的判定、三角形中位线的性质以及直角三角形斜边上的中线的性质.注意证得EF=DG=$\frac{1}{2}$AB是关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
12. 如图,直线AB、CD相交于点E,那么下列结论正确的是( )
如图,直线AB、CD相交于点E,那么下列结论正确的是( )
 如图,直线AB、CD相交于点E,那么下列结论正确的是( )
如图,直线AB、CD相交于点E,那么下列结论正确的是( )| A. | ∠AEC与∠CEB互为余角 | B. | ∠BED与∠CEB互为余角 | ||
| C. | ∠CEB与∠BED互为余角 | D. | ∠AEC与∠BED是对顶角 |
9.下列根式中属最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{8}$ |
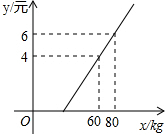 某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围.
某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围. 如图,已知∠α、∠β,用直尺和圆规求作一个∠AOB,使得∠AOB=2∠α-∠β(不写作法,保留作图痕迹).
如图,已知∠α、∠β,用直尺和圆规求作一个∠AOB,使得∠AOB=2∠α-∠β(不写作法,保留作图痕迹). 甲乙两车分别从A、B两地同时出发,相向而行,甲车以m千米/时的速度从A地匀速驶往B地,到达B地后停留在B地;乙车以n千米/时的速度从B地匀速驶往A地,到达A地后,立即以2n千米/时的速度沿原路匀速返回B地,设两车相距y(千米),乙车行驶时间为t(时),两车从出发至乙车到达A地过程中y与t的图象如图所示.
甲乙两车分别从A、B两地同时出发,相向而行,甲车以m千米/时的速度从A地匀速驶往B地,到达B地后停留在B地;乙车以n千米/时的速度从B地匀速驶往A地,到达A地后,立即以2n千米/时的速度沿原路匀速返回B地,设两车相距y(千米),乙车行驶时间为t(时),两车从出发至乙车到达A地过程中y与t的图象如图所示.