Question

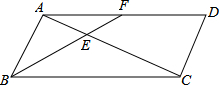如图，在平行四边形ABCD中，点F是AD边上一点，连接BF与对角线AC相交于点E．
①

AF

AD

=

1

2

时，

S△ABF

S?ABCD

=

 

．
②当

AF

AD

=

m

n

时，

S△ABF

S?ABCD

=

 

，

S△AEF

S?ABCD

=

 

．

Answer 1

考点：平行四边形的性质,相似三角形的判定与性质

专题：

分析：①根据三角形的面积公式和平行四边形的面积公式进行解答即可；
②利用相似三角形：△AEF∽△CEB的性质来求

S△AEF

S?ABCD

的值．

解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△ABF与?ABCD同高．
①∵

AF

AD

=

1

2

，
∴

S△ABF

S?ABCD

=

1 2 AF

AD

=

1

4

．
故答案是：

1

4

．
②如图，过点作GH⊥AD，交AD于点G，交BC于点H，则EH⊥BC．
∵

AF

AD

=

m

n

，
∴

S△ABF

S?ABCD

=

1 2 AF

AD

=

1

2

•

m

n

=

m

2n

．
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC．
∴△AEF∽△CEB，
∴

GE

EH

=

AF

BC

=

AF

AD

=

m

n

，
∴

GE

GH

=

m

m+n

，

S△AEF

S?ABCD

=

1 2 AE•EG

AD•GH

=

1 2 AF•EG

AD•GH

=

1

2

•

m

n

•

m

m+n

=

m2

2n(m+n)

．
故答案是：

m

2n

；

m2

2n(m+n)

．

点评：本题考查了平行四边形的判定和相似三角形的判定与性质．此题利用了相似三角形的对应边上的高对应成比例．