题目内容
若|a+6|+（b-2）2=0，则ab的值为 ．
考点：非负数的性质：偶次方,非负数的性质：绝对值
专题：
分析：根据非负数的性质，可求出a、b的值，然后将代数式化简再代值计算．
解答：解：∵|a+6|+（b-2）2=0，
∴a+6=0，b-2=0，
解得a=-6，b=2，
∴ab=（-6）2=36；
故答案为36．
∴a+6=0，b-2=0，
解得a=-6，b=2，
∴ab=（-6）2=36；
故答案为36．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
下列说法中错误的是（ ）
| A、-12的绝对值是12 |
| B、绝对值等于12的数只有12 |
| C、+12的绝对值等于12 |
| D、+12、-12的绝对值相等 |
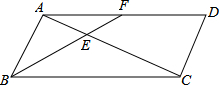如图，在平行四边形ABCD中，点F是AD边上一点，连接BF与对角线AC相交于点E．
如图，CD平分ACE，且∠B=∠ACD，则得出的结论是（ ）| A、AD∥BC |
| B、AB∥CD |
| C、AC平分∠BCD |
| D、CA平分∠BAD |