题目内容
通分:
,
,
.
| 1 |
| 2m2+3m |
| 2 |
| 3-2m |
| 2m+5 |
| 4m2-9 |
考点:通分
专题:计算题
分析:先把各分式的分母因式分解,则可确定最简公分母,然后根据分式的基本性质把各分式的分母都化为最简公分母即可.
解答:解:最简公分母为m(2m+3)(2m-3),
=
=
,
=-
=-
,
=
=
.
| 1 |
| 2m2+3m |
| 1 |
| m(2m+3) |
| 2m-3 |
| m(2m+3)(2m-3) |
| 2 |
| 3-2m |
| 2 |
| 2m-3 |
| 2m(2m+3) |
| m(2m+3)(2m-3) |
| 2m+5 |
| 4m2-9 |
| 2m+5 |
| (2m+3)(2m-3) |
| m(2m+5) |
| m(2m+3)(2m-3) |
点评:本题考查了通分:把几个异分母的分式分别化为与原来的分式相等的同分母的分式,这样的分式变形叫做分式的通分.通分的关键是确定最简公分母.

练习册系列答案
相关题目
 如图,CD平分ACE,且∠B=∠ACD,则得出的结论是( )
如图,CD平分ACE,且∠B=∠ACD,则得出的结论是( )| A、AD∥BC |
| B、AB∥CD |
| C、AC平分∠BCD |
| D、CA平分∠BAD |
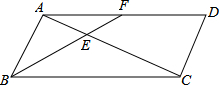 如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E.
如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E. 如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC.
如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC. 如图,已知∠ADE=60°,∠1=30°,请你添加一个条件,使得能利用“内错角相等,两直线平行”来判断BE∥DF,你添加的条件是
如图,已知∠ADE=60°,∠1=30°,请你添加一个条件,使得能利用“内错角相等,两直线平行”来判断BE∥DF,你添加的条件是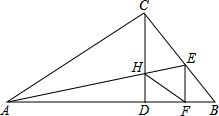 如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形.
如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形.