题目内容
若(a+1)2+|b-2013|=0,则ab= .
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
解答:解:∵(a+1)2+|b-2013|=0,
∴a+1=0,b-2013=0,
∴a=-1,b=2013,
∴ab=(-1)2013=-1.
故答案为-1.
∴a+1=0,b-2013=0,
∴a=-1,b=2013,
∴ab=(-1)2013=-1.
故答案为-1.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
关于函数y=x2的性质表达正确的一项是( )
| A、无论x为任何实数,y值总为正 |
| B、当x值增大时,y的值也增大 |
| C、它的图象关于y轴对称 |
| D、它的图象在第一、三象限内 |
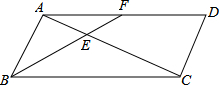 如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E.
如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E. 如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC.
如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC.