题目内容
 如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为
如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为考点:翻折变换(折叠问题),三角形中位线定理
专题:几何图形问题
分析:根据对称轴垂直平分对应点连线,可得AF即是△ABC的高,再由中位线的性质求出BC,继而可得△ABC的面积.
解答: 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,
∴DE∥BC,BC=2DE=10cm;
由折叠的性质可得:AF⊥DE,
∴AF⊥BC,
∴S△ABC=
BC×AF=
×10×8=40cm2.
故答案为:40.
 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,∴DE∥BC,BC=2DE=10cm;
由折叠的性质可得:AF⊥DE,
∴AF⊥BC,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:40.
点评:本题考查了翻折变换的性质及三角形的中位线定理,解答本题的关键是得出AF是△ABC的高.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 如图,已知抛物线y=
如图,已知抛物线y=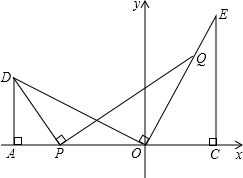 如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q;
如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q; 如图,在直角坐标系中,已知点A(-3,-1),点B(-2,1),平移线段AB,使点A落在A1(0,-1),点B落在点B1,则点B1的坐标为
如图,在直角坐标系中,已知点A(-3,-1),点B(-2,1),平移线段AB,使点A落在A1(0,-1),点B落在点B1,则点B1的坐标为