题目内容
 如图,已知抛物线y=
如图,已知抛物线y=| 3 |
| 8 |
| 3 |
| 4 |
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)令y=0,解方程
x2-
x-3=0可得到A点和D点坐标;令x=0,求出y=-3,可确定C点坐标;
(2)根据抛物线的对称性,可知在在x轴下方对称轴右侧也存在这样的一个点;再根据三角形的等面积法,在x轴上方,存在两个点,这两个点分别到x轴的距离等于点C到x轴的距离;
(3)根据梯形定义确定点P,如图所示:①若BC∥AP1,确定梯形ABCP1.此时P1与D点重合,即可求得点P1的坐标;②若AB∥CP2,确定梯形ABCP2.先求出直线CP2的解析式,再联立抛物线与直线解析式求出点P2的坐标.
| 3 |
| 8 |
| 3 |
| 4 |
(2)根据抛物线的对称性,可知在在x轴下方对称轴右侧也存在这样的一个点;再根据三角形的等面积法,在x轴上方,存在两个点,这两个点分别到x轴的距离等于点C到x轴的距离;
(3)根据梯形定义确定点P,如图所示:①若BC∥AP1,确定梯形ABCP1.此时P1与D点重合,即可求得点P1的坐标;②若AB∥CP2,确定梯形ABCP2.先求出直线CP2的解析式,再联立抛物线与直线解析式求出点P2的坐标.
解答:解:(1)∵y=
x2-
x-3,
∴当y=0时,
x2-
x-3=0,
解得x1=-2,x2=4.
当x=0,y=-3.
∴A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)∵y=
x2-
x-3,
∴对称轴为直线x=
=1.
∵AD在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,-3),
∴M点坐标为(2,-3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.
当y=3时,
x2-
x-3=3,
解得x1=1+
,x2=1-
,
∴M点坐标为(1+
,3)或(1-
,3).
综上所述,所求M点坐标为(2,-3)或(1+
,3)或(1-
,3);
 (3)结论:存在.
(3)结论:存在.
如图所示,在抛物线上有两个点P满足题意:
①若BC∥AP1,此时梯形为ABCP1.
由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,
∴P1(-2,0).
∵P1A=6,BC=2,
∴P1A≠BC,
∴四边形ABCP1为梯形;
 ②若AB∥CP2,此时梯形为ABCP2.
②若AB∥CP2,此时梯形为ABCP2.
∵A点坐标为(4,0),B点坐标为(2,-3),
∴直线AB的解析式为y=
x-6,
∴可设直线CP2的解析式为y=
x+n,
将C点坐标(0,-3)代入,得n=-3,
∴直线CP2的解析式为y=
x-3.
∵点P2在抛物线y=
x2-
x-3上,
∴
x2-
x-3=
x-3,
化简得:x2-6x=0,
解得x1=0(舍去),x2=6,
∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,
∴P2(6,6).
∵AB∥CP2,AB≠CP2,
∴四边形ABCP2为梯形.
综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
| 3 |
| 8 |
| 3 |
| 4 |
∴当y=0时,
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=-2,x2=4.
当x=0,y=-3.
∴A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)∵y=
| 3 |
| 8 |
| 3 |
| 4 |
∴对称轴为直线x=
| ||
2×
|
∵AD在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,-3),
∴M点坐标为(2,-3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.
当y=3时,
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=1+
| 17 |
| 17 |
∴M点坐标为(1+
| 17 |
| 17 |
综上所述,所求M点坐标为(2,-3)或(1+
| 17 |
| 17 |
 (3)结论:存在.
(3)结论:存在.如图所示,在抛物线上有两个点P满足题意:
①若BC∥AP1,此时梯形为ABCP1.
由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,
∴P1(-2,0).
∵P1A=6,BC=2,
∴P1A≠BC,
∴四边形ABCP1为梯形;
 ②若AB∥CP2,此时梯形为ABCP2.
②若AB∥CP2,此时梯形为ABCP2.∵A点坐标为(4,0),B点坐标为(2,-3),
∴直线AB的解析式为y=
| 3 |
| 2 |
∴可设直线CP2的解析式为y=
| 3 |
| 2 |
将C点坐标(0,-3)代入,得n=-3,
∴直线CP2的解析式为y=
| 3 |
| 2 |
∵点P2在抛物线y=
| 3 |
| 8 |
| 3 |
| 4 |
∴
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 2 |
化简得:x2-6x=0,
解得x1=0(舍去),x2=6,
∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,
∴P2(6,6).
∵AB∥CP2,AB≠CP2,
∴四边形ABCP2为梯形.
综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线与坐标轴的交点坐标求法,三角形的面积,梯形的判定.综合性较强,有一定难度.运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
相关题目
下图能说明∠1>∠2的是( )
A、 |
B、 |
C、 |
D、 |
 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)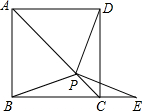 如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.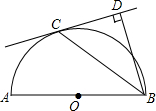 如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA. 如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为
如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为