题目内容
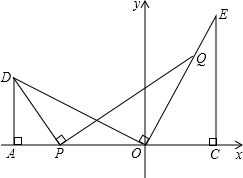 如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q;
如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q;(1)求D、E的坐标;
(2)当点P与A,O两点不重合时,求
| DP |
| PQ |
(3)当点P从A点运动到AO的中点时,求线段DQ的中点移动路径(线段)的图象的解析式,并写出自变量的取值范围.
考点:一次函数综合题
专题:综合题
分析:(1)由OD垂直于OE,得到一对角互余,再由∠ECA=90°,得到直角三角形EOC两锐角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,且AD=OC,利用AAS得到三角形AOD与三角形EOC全等,利用全等三角形对应边相等得到AO=CE=6,再由OC=AD=3,即可确定出D与E的坐标;
(2)连接DQ,由DP垂直于PQ,DO垂直于OE,得到D,P,O,Q四点共圆,利用圆周角定理得到∠DQP=∠DOA,再直角三角形AOD中,利用锐角三角函数定义即可求出所求式子的值;
(3)当点P与点A重合时,DQ的中点即是DO的中点M,假设当点P在AO中点时,DQ的中点为点N,则线段DQ的中点所经过的路径(线段)就是△ODQ的中位线MN,根据D坐标确定出M坐标,根据E坐标确定出N坐标,设直线MN解析式为y=kx+b,将M,N坐标代入求出k与b的值,确定出直线MN解析式,即可得出线段DQ的中点移动路径(线段)的图象的解析式,以及自变量的取值范围.
(2)连接DQ,由DP垂直于PQ,DO垂直于OE,得到D,P,O,Q四点共圆,利用圆周角定理得到∠DQP=∠DOA,再直角三角形AOD中,利用锐角三角函数定义即可求出所求式子的值;
(3)当点P与点A重合时,DQ的中点即是DO的中点M,假设当点P在AO中点时,DQ的中点为点N,则线段DQ的中点所经过的路径(线段)就是△ODQ的中位线MN,根据D坐标确定出M坐标,根据E坐标确定出N坐标,设直线MN解析式为y=kx+b,将M,N坐标代入求出k与b的值,确定出直线MN解析式,即可得出线段DQ的中点移动路径(线段)的图象的解析式,以及自变量的取值范围.
解答:解:(1)∵OD⊥OE,
∴∠AOD+∠COE=180°-90°=90°,
∵∠ECA=90°,
∴∠COE+∠E=180°-90°=90°,
∴∠AOD=∠E,
在△AOD和△CEO中,
,
∴△AOD≌△CEO(AAS),
∴AO=CE=6,
∵OC=AD=3,
∴D(-6,3),E(3,6);
(2)连结DQ,如图1所示,

∵OD⊥OE,DP⊥PQ,
∴∠DPQ=∠DBQ=90°,
∴点D、P、O、Q都在以DQ为直径的圆上,
∴∠DQP=∠DOA,
∵tan∠DQP=tan∠DOA,
∴
=
=
=
;
(3)当点P与点A重合时,DQ的中点即是DO的中点M,
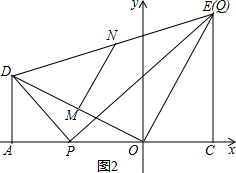
假设当点P在AO中点时,DQ的中点为点N,则线段DQ的中点所经过的路径(线段)就是△ODQ的中位线MN,
∵点D(-6,3),
∴点M(-3,1.5),
∵当点P在AO中点时,点Q与点E重合.
∴点E(3,6),
∴点N(-1.5,4.5),
设直线MN的解析式为y=kx+b,
把点M、N代入得:
,
解得:k=2,b=7.5,
∴直线MN解析式为y=2x+7.5,
则线段DQ中点移动路径的图象解析式为y=2x+7.5(-3≤x≤-1.5).
∴∠AOD+∠COE=180°-90°=90°,
∵∠ECA=90°,
∴∠COE+∠E=180°-90°=90°,
∴∠AOD=∠E,
在△AOD和△CEO中,
|
∴△AOD≌△CEO(AAS),
∴AO=CE=6,
∵OC=AD=3,
∴D(-6,3),E(3,6);
(2)连结DQ,如图1所示,

∵OD⊥OE,DP⊥PQ,
∴∠DPQ=∠DBQ=90°,
∴点D、P、O、Q都在以DQ为直径的圆上,
∴∠DQP=∠DOA,
∵tan∠DQP=tan∠DOA,
∴
| DP |
| PQ |
| DA |
| AO |
| 3 |
| 6 |
| 1 |
| 2 |
(3)当点P与点A重合时,DQ的中点即是DO的中点M,

假设当点P在AO中点时,DQ的中点为点N,则线段DQ的中点所经过的路径(线段)就是△ODQ的中位线MN,
∵点D(-6,3),
∴点M(-3,1.5),
∵当点P在AO中点时,点Q与点E重合.
∴点E(3,6),
∴点N(-1.5,4.5),
设直线MN的解析式为y=kx+b,
把点M、N代入得:
|
解得:k=2,b=7.5,
∴直线MN解析式为y=2x+7.5,
则线段DQ中点移动路径的图象解析式为y=2x+7.5(-3≤x≤-1.5).
点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,待定系数法确定一次函数解析式,熟练掌握待定系数法是解本题第三问的关键.

练习册系列答案
相关题目
 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. 如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA. 如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β=
如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β= 如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为
如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为