题目内容
已知m,n是方程x2+2x-5=0的两个实数根,则m2-mn+3m+n= .
考点:根与系数的关系,一元二次方程的解
专题:常规题型
分析:根据m+n=-
=-2,m•n=-5,直接求出m、n即可解题.
| b |
| a |
解答:解:∵m、n是方程x2+2x-5=0的两个实数根,
∴mn=-5,m+n=-2,
∵m2+2m-5=0
∴m2=5-2m
m2-mn+3m+n=(5-2m)-(-5)+3m+n
=10+m+n
=10-2
=8
故答案为:8.
∴mn=-5,m+n=-2,
∵m2+2m-5=0
∴m2=5-2m
m2-mn+3m+n=(5-2m)-(-5)+3m+n
=10+m+n
=10-2
=8
故答案为:8.
点评:此题主要考查了一元二次方程根根的计算公式,根据题意得出m和n的值是解决问题的关键.

练习册系列答案
相关题目
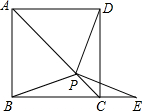 如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC. 如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β=
如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β= 如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为
如图,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为 如图,直线a、b被直线c所截,若满足
如图,直线a、b被直线c所截,若满足