题目内容
3.已知$\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}$,则$\frac{(a+b)(b+c)(c+a)}{abc}$的值为( )| A. | 8 | B. | 1 | C. | -1或8 | D. | -1或1 |
分析 设已知等式等于k,得出三个关系式,结合后化简得到a+b+c=0或k=1,即可确定出原式的值.
解答 解:设$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$=k,
可得a+b-c=ck①,a-b+c=bk②,-a+b+c=ak③,
①+②+③得:2(a+b+c)=(k+1)(a+b+c),
整理得:(a+b+c)(2-k-1)=0,
可得a+b+c=0或1-k=0,
若a+b+c=0,可得-2c=ck,即k=-2,
此时原式=$\frac{c(k+1)b(k+1)a(k+1)}{abc}$=(k+1)3=-1;
若k=1,原式=(k+1)3=8.
故选C
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
 如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
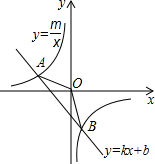 如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点; 如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).
如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).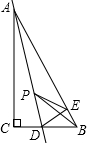 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.