题目内容
12. 如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).
如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的位置开始,将△ABC绕着点A顺时针旋转,设旋转角为α(0°<α<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF(如图2).已知∠BAC=60°,∠C=90°,AC=8,⊙O的直径为8.在旋转过程中,有以下几个量:①弦EF的长 ②弧EF的长 ③∠AFE的度数 ④点O到EF的距离.其中不变的量是①②④(只填正确答案序号).
分析 在整个旋转过程中,∠A为弦切角或圆周角,且大小不变,所以其所对的弦、弧不变;在整个旋转过程中,∠AEF和∠AFE都在改变,大小不能确定.
解答 解:∵在整个旋转过程中,∠A为圆周角,且大小不变,所以其所对的弦、弧不变;
∴①②正确;
过点O作OG⊥EF,垂足为G.
∵DG⊥EF,
∴GF=EG=$\frac{1}{2}EF$.
在Rt△OFG中,由勾股定理得:OG=$\sqrt{O{F}^{2}-F{G}^{2}}$=$\sqrt{O{F}^{2}-(\frac{1}{2}EF)^{2}}$,
∵OF不变,EF不变,
∴点O到EF的距离不变.
∴④正确.
∵在整个旋转过程中,∠AEF和∠AFE都在改变,大小不能确定,
∴∠AFE的度数不断变化.
∴③错误.
故答案为:①②④.
点评 此题综合考查了旋转的性质及圆的有关性质的应用,由旋转的性质得到∠A为定值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知$\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}$,则$\frac{(a+b)(b+c)(c+a)}{abc}$的值为( )
| A. | 8 | B. | 1 | C. | -1或8 | D. | -1或1 |
1.下列句子,不一定正确的是( )
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |

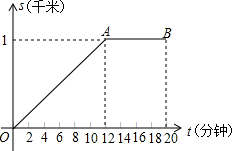 小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.
小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.