题目内容
18.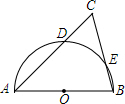 如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$.
如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$.(1)求证:△CDE∽△CBA;
(2)求DE的长.
分析 (1)由圆内接四边形的外角等于它的内对角知∠CED=∠A(或∠CDE=∠B),又有∠C=∠C,故△CDE∽△CBA;
(2)连接AE.由(1)中△CDE∽△CBA得DE:BA=CE:CA,由于直径对的圆周角是直角,有∠AEB=∠AEC=90°;在Rt△AEC中,有∠C=60°,∠CAE=30°.则DE:BA=CE:CA=1:2,即DE=$\sqrt{3}$.
解答 (1)证明:∵四边形ABED为⊙O的内接四边形,
∴∠CED=∠A(或∠CDE=∠B);
又∠C=∠C,
∴△CDE∽△CBA.
(2)解:连接AE.
由(1)得△CDE∽△CBA,
∴$\frac{DE}{BA}$=$\frac{CE}{CA}$,
∵AB为⊙O的直径,
∴∠AEB=∠AEC=90°.
在Rt△AEC中,
∵∠C=60°,
∴∠CAE=30°;
∴$\frac{DE}{BA}$=$\frac{CE}{CA}$=$\frac{1}{2}$,即DE=$\sqrt{3}$.
点评 本题考查了圆内接四边形的性质、相似三角形的判定和性质、圆周角定理,直角三角形的性质等知识的综合应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.“直角都相等”与“相等的角是直角”是( )
| A. | 互为逆命题 | B. | 互逆定理 | C. | 公理 | D. | 假命题 |
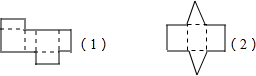 下面是两种立体图形的展开图.请分别写出这两个立体图形的名称:
下面是两种立体图形的展开图.请分别写出这两个立体图形的名称: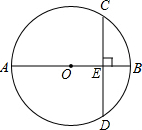 如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.
如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm. 如图,在正方形ABCD中,M为DC上一定点,N是AC上的一动点,要使DN+MN最小,请找出N点的位置.
如图,在正方形ABCD中,M为DC上一定点,N是AC上的一动点,要使DN+MN最小,请找出N点的位置.