题目内容
10.若x2-4x+1=0,则(1)x2+$\frac{1}{{x}^{2}}$的值为14;
(2)x-$\frac{1}{x}$的值为±2$\sqrt{3}$.
分析 (1)先将原式变形为x+$\frac{1}{x}$=4,然后两边平方,再移项就可以求出结论;
(2)先求出$(x-\frac{1}{x})^{2}$,再开方,即可解答.
解答 解:(1)x2-4x+1=0,
∵x≠0,
∴x-4+$\frac{1}{x}$=0,
∴x+$\frac{1}{x}$=4,
∴$(x+\frac{1}{x})^{2}={4}^{2}$
${x}^{2}+2+\frac{1}{{x}^{2}}=16$
${x}^{2}+\frac{1}{{x}^{2}}=14$.
故答案为:14;
(2)$(x-\frac{1}{x})^{2}=(x+\frac{1}{x})^{2}-4$=42-4=12,
x-$\frac{1}{x}$=±2$\sqrt{3}$.
故答案为:±2$\sqrt{3}$.
点评 本题考查了完全平分公式,解决本题的关键是熟记完全平分公式.

练习册系列答案
相关题目
20.当已知A(-2,y1),B(-1,y2),C(-5,y3)在抛物线y=-$\frac{1}{2}$x2-3x-π上,则y1,y2,y3之间的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2=y3<y1 | D. | y3<y2<y1 |
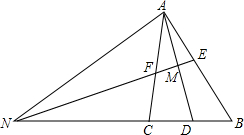 已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.
已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.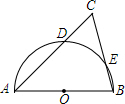 如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$.
如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$.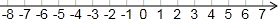 在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)
在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)