题目内容
18．若关于x的分式方程$\frac{x-1}{x-2}=\frac{m}{x-2}+3$无解，则m的值为1．分析 根据分式方程无解，可得分式方程的增根，根据分式方程的增根适合整式方程，可得关于m的方程，根据解方程，可得答案．
解答 解：两边都乘以（x-2），得
x-1=m+3（x-2）．
m=-2x+5．
分式方程的增根是x=2，
将x=2代入，得
m=-2×2=5=1，
故答案为：1．
点评 本题考查了分式方程的解，将分式方程的增根代入整式方程得出关于m的方程是解题关键．
练习册系列答案
相关题目
13．
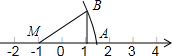如图，Rt△MBC中，∠MCB=90°，点M在数轴-1处，点C在数轴1处，MA=MB，BC=1，则数轴上点A对应的数是（ ）
如图，Rt△MBC中，∠MCB=90°，点M在数轴-1处，点C在数轴1处，MA=MB，BC=1，则数轴上点A对应的数是（ ）| A． | $\sqrt{5}$+1 | B． | -$\sqrt{5}$+1 | C． | -$\sqrt{5}$-l | D． | $\sqrt{5}$-1 |
3．
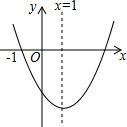已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（ ）| A． | ac＞0 | B． | 当x＞-1时，y＜0 | C． | b=2a | D． | 9a+3b+c=0 |
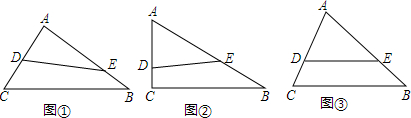
如图，一个圆锥的底面半径为2cm，侧面展开图是半圆．则圆锥的母线长为4cm．