题目内容
3.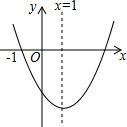 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>-1时,y<0 | C. | b=2a | D. | 9a+3b+c=0 |
分析 A、由抛物线的开口方向,抛物线与y轴交点的位置即可确定a、c的符号;
B、根据抛物线与x轴的交点,可得出y<0时,x的取值范围;
C、根据抛物线的对称轴直接得出答案;
D、根据抛物线与x轴的交点和抛物线的对称轴,即可得出抛物线与x轴的另一个交点,然后把x=3代入方程即可求得相应的y的符号.
解答 解:A、由抛物线的开口向上,得a>0,抛物线与y轴负半轴相交,得c<0,则ac<0,故本选项错误;
B、根据抛物线与x轴的交点,可得出y<0时,-1<x<3,故本选项错误;
C、根据抛物线的对称轴x=-$\frac{b}{2a}$=1,直接得出b=-2a,故本选项错误;
D、根据抛物线与x轴的一个交点(-1,0)和抛物线的对称轴x=1,即可得出抛物线与x轴的另一个交点(3,0),然后把x=3代入方程即9a+3b+c=0,故本选项正确;
故选D.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
13. 如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
 如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
14.下列计算正确的是( )
| A. | a5+a5=a10 | B. | 3a5•2a3=6a8 | C. | a10÷a2=a5 | D. | (3a4)3=9a12 |
4. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )| A. | DF⊥AB | B. | CG=2GA | C. | CG=DF+GE | D. | S四边形BFGC=$\sqrt{3}$-1 |
 如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°.
如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°.