题目内容
a2-6a+18有没有最大或者最小值？若有，请求出：当a取何值时，最大（小）值是多少？
考点：配方法的应用,非负数的性质：偶次方
专题：计算题
分析：原式前两项配方变形后，利用非负数的性质求出
解答：解：∵（x-3）2≥0，
∴a2-6a+18=a2-6a+9+9=（a-3）2+9≥9，
则a=3时，原式取得最小值9．
∴a2-6a+18=a2-6a+9+9=（a-3）2+9≥9，
则a=3时，原式取得最小值9．
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
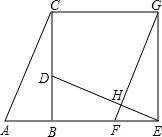如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．
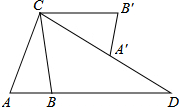如图，在△ABC中，AB=2，AC=4，将△ABC绕点C按逆时针方向旋转得到△A′B′C，使CB′∥AB，分别延长AB、CA′相交于点D，则线段BD的长为
如图，⊙O的半径为3，P是CB延长线上一点，PO=5，PA切⊙O于A点，则PA=
如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是