题目内容
 如图,将面积为a2的小正方形和面积为b2的大正方形放在一起(b>a>0),用a,b表示△ABC的面积为
如图,将面积为a2的小正方形和面积为b2的大正方形放在一起(b>a>0),用a,b表示△ABC的面积为考点:列代数式
专题:
分析:要求△ABC的面积,求△ABH的面积和△AEH的面积和△BEC的面积,且存在等量关系,△AEH的面积和△BEC的面积等于a2+b2减去△AFC和△BCG的面积,根据此等量关系求解.
解答:解:由题图可知:
S△ABC=S△ABH+S△AEH+S△BEC.
且S△AEH+S△BEC=a2+b2-S△AFC-S△BDG.
S△AFC=
,
S△BDG=
,
∴S△ABC=S△ABH+a2+b2-S△AFC-S△BDG
=
+a2+b2-
-
=
.
故答案为:
.
S△ABC=S△ABH+S△AEH+S△BEC.
且S△AEH+S△BEC=a2+b2-S△AFC-S△BDG.
S△AFC=
| a(a+b) |
| 2 |
S△BDG=
| b2 |
| 2 |
∴S△ABC=S△ABH+a2+b2-S△AFC-S△BDG
=
| a(b-a) |
| 2 |
| a(a+b) |
| 2 |
| b2 |
| 2 |
| b2 |
| 2 |
故答案为:
| b2 |
| 2 |
点评:本题考查了三角形面积计算公式,考查了正方形四边均相等,且邻边互相垂直的性质,本题中将求△AEH的面积和△BEC的面积转化到两个正方形面积减去△AFC和△BCG的面积是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
下列实数中,是无理数的是( )
A、
| |||
| B、-0.3 | |||
C、
| |||
D、
|
如果有理数a,b,c满足关系式a<b<0<c,那么式子
的值( )
| bc-ac |
| ab2c2 |
| A、必为正数 | B、必为负数 |
| C、可正可负 | D、可能为0 |
 如图,长方形的长为(6a+2)cm,宽(3a+3)cm,已知长比宽多11cm,则长方形的长为
如图,长方形的长为(6a+2)cm,宽(3a+3)cm,已知长比宽多11cm,则长方形的长为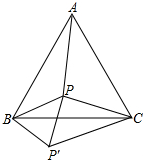 已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.
已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.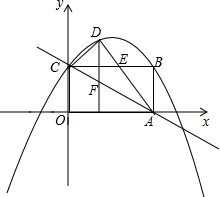 已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0,
已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0,