题目内容
17.已知等腰直角三角形ABC斜边BC的长为2,△DBC为等边三角形,那么A,D两点的距离为$\sqrt{3}$+1或$\sqrt{3}$-1.分析 分两种情况:①连接AD,由等边三角形等腰三角形的性质得出AD垂直平分BC,由直角三角形斜边上的中线性质得出AE=$\frac{1}{2}$BC=1,由勾股定理求出DE,即可得出AD;②由①得:DE=$\sqrt{3}$,AE=1,AD=DE=AD,即可得出结果.
解答 解:分两种情况:
①如图1所示:
连接AD,交BC于E,
∵△DBC为等边三角形,
∴BD=CD=BC=2,
∵AB=AC,
∴AD垂直平分BC,
∴AE=$\frac{1}{2}$BC=1,∠DEB=90°, ∴DE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴DE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AD=DE+AE=$\sqrt{3}$-1;
②如图2所示:
由①得:DE=$\sqrt{3}$,AE=1,
∴AD=DE=AD=$\sqrt{3}$-1;
综上所述:A,D两点的距离为$\sqrt{3}$+1或$\sqrt{3}$-1;
故答案为:$\sqrt{3}$+1或$\sqrt{3}$-1.
点评 本题考查了勾股定理、等边三角形的性质、等腰直角三角形的性质、直角三角形斜边上的中线性质;熟练掌握等边三角形和等腰直角三角形的性质,由勾股定理求出DE是解题的关键.

练习册系列答案
相关题目
11.下列各组数的大小比较,正确的是( )
| A. | -8>0 | B. | -20>-10 | C. | -$\frac{3}{5}$$<-\frac{4}{5}$ | D. | -$\frac{2}{3}$$>-\frac{3}{4}$ |
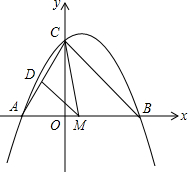 如图,二次函数y=-$\frac{1}{2}$x2+x+4与x轴交于A、B两点,与y轴交于点C.
如图,二次函数y=-$\frac{1}{2}$x2+x+4与x轴交于A、B两点,与y轴交于点C.