题目内容
11.有这样一道题“当a=2,b=-3时,求多项式a2b3-$\frac{1}{2}$ab+b2-(-4a2b3-$\frac{1}{4}$ab-b2)+(3a2b3+$\frac{1}{4}$ab)-5的值”,小胡做题时把a=2错抄成a=-2,但他作出的结果却是正确的,你知道这是怎么回事吗?说明理由,并求出结果.分析 原式去括号合并得到最简结果,即可作出判断.
解答 解:原式=a2b3-$\frac{1}{2}$ab+b2+4a2b3+$\frac{1}{4}$ab+b2+3a2b3+$\frac{1}{4}$ab-5=2b2-5,
结果与a的取值无关,故小胡做题时把a=2错抄成a=-2,但他作出的结果却是正确的,
当a=2或a=-2,b=-3时,原式=2b2-5=2×9-5=13.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.已知二次函数y=mx2+x+m(m+1)的图象经过原点,则m的值为( )
| A. | 0或-1 | B. | 0 | C. | -1 | D. | 无法确定 |
2. 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )| A. | 6$\sqrt{3}$+12 | B. | 6$\sqrt{3}$+16 | C. | 18 | D. | 6 |
 由几个大小相同的正方形组成的几何图形如图,则它的左视图是( )
由几个大小相同的正方形组成的几何图形如图,则它的左视图是( )



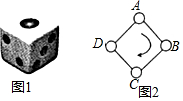 如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字1,2,3,4,5,6,如图2,正方形ABCD的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落在圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落得圈B;…设游戏者从圈A起跳.
如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字1,2,3,4,5,6,如图2,正方形ABCD的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落在圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落得圈B;…设游戏者从圈A起跳.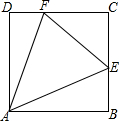 如图,四边形ABCD为正方形(各边相等,各内角为直角),E是BC边上一点,F是CD上的一点.
如图,四边形ABCD为正方形(各边相等,各内角为直角),E是BC边上一点,F是CD上的一点.