Question

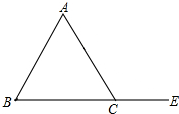已知如图：△ABC是等边三角形，边长为1，延长BC到E，使得CE=

1

2

BC．
（1）用尺规作图的方法，过点B作BD⊥AC，垂足为点D，连接DE；（不写作法，保留作图痕迹）
（2）求证：△DBE为等腰三角形．

Answer 1

考点：含30度角的直角三角形,等腰三角形的判定,作图—基本作图

专题：

分析：（1）按照过直线外一点作已知直线的垂线的步骤作BD⊥AC于点D，再连接DE即可；
（2）先由△ABC是等边三角形，得出∠ABC=∠ACB=60°，AB=BC=AC．根据等腰三角形三线合一的性质得出∠DBC=

1

2

∠ABC=30°，CD=

1

2

AC，由CE=

1

2

BC，AC=BC，等量代换得出CD=CE，再根据等边对等角及三角形外角的性质得出∠E=∠CDE=

1

2

∠ACB=30°，于是∠DBC=∠E=30°，然后根据等角对等边得到DE=DB，即△DBE为等腰三角形．

解答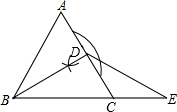：（1）解：如图所示：

（2）证明：∵△ABC是等边三角形，
∴∠ABC=∠ACB=60°，AB=BC=AC．
∵AB=BC，BD⊥AC于点D，
∴∠DBC=

1

2

∠ABC=30°，CD=

1

2

AC，
∵CE=

1

2

BC，AC=BC，
∴CD=CE，
∴∠E=∠CDE=

1

2

∠ACB=30°，
∴∠DBC=∠E=30°，
∴DE=DB，
∴△DBE为等腰三角形．

点评：本题考查了过直线外一点作已知直线的垂线，等腰三角形的判定与性质，等边三角形的性质，熟知等腰三角形三线合一的性质是解答（2）题的关键．