题目内容
1.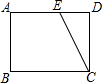 如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为3或6.
如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为3或6.
分析 如图1,所示,由∠CFE+∠AFE=180°,可知点A、F、C在一条直线上,先求得AC的长,然后由△AEF∽△ACD可求得ED的长;如图2所示,可证明四边形CDEF为正方形从而可求得ED的长.
解答 解:如图1所示: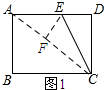
由翻折的性质可知:EF=ED,∠EFC=∠EDC=90°,
∵△AEF为直角△,
∴∠AFE=90°.
∴∠CFE+∠AFE=180°.
∴点A、F、C在一条直线上.
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{6}^{2}+{8}^{2}}$=10.
设DE=x,则EF=x.
∵∠EAF=∠DAC,∠EFA=∠CDA,
∴△AEF∽△ACD.
∴$\frac{EF}{DC}=\frac{AE}{AC}$,即$\frac{x}{6}=\frac{8-x}{10}$.
解得:x=3.
∴ED=3.
如图2所示: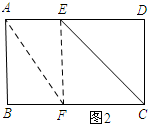
∵∠AEF=90°,
∴∠FED=90°.
∴∠FED=∠D=∠DCF=90°.
∴四边形CDEF为矩形.
由翻折的性质可知:DE=EF.
∴四边形CDEF为正方形.
∴DE=DC=6.
综上所述,ED的长为3或6.
故答案为:3或6.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理、矩形、正方形的性质和判定,根据题意画出图形是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
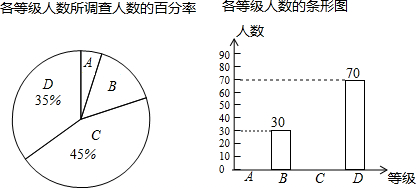
16.某校七年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个)
统计发现两班总分相等,S${\;}_{甲}^{2}$$<{S}_{乙}^{2}$,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)根椐以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 合计 | |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)根椐以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
6.下列代数式的书写格式正确的是( )
| A. | 1$\frac{1}{2}$abc | B. | a•b÷4+3 | C. | 3xy÷8 | D. | -$\frac{3}{4}$mn |
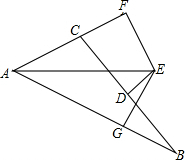 如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证:
如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证: