题目内容
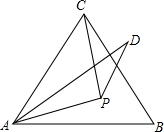 已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.
已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:连接PB,求出AD=AB,根据SAS推出△DAP≌△BAP,根据全等推出∠ADP=∠ABP,根据SSS推出△CBP≌△ABP,根据全等三角形的性质得出∠CBP=∠ABP,即可得出答案.
解答:证明:如图,连接PB,
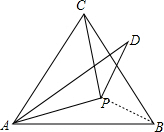
∵△ABC是等边三角形,
∴∠CBA=60°,AC=BC=AB,
∵AD=AC,
∴AD=AB,
在△DAP和△BAP中,
,
∴△DAP≌△BAP(SAS),
∴∠ADP=∠ABP,
在△CBP和△ABP中,
,
∴△CBP≌△ABP(SSS),
∴∠CBP=∠ABP,
∵∠ABC=60°,∠ADP=∠ABP,
∴∠ADP=∠ABP=30°.

∵△ABC是等边三角形,
∴∠CBA=60°,AC=BC=AB,
∵AD=AC,
∴AD=AB,
在△DAP和△BAP中,
|
∴△DAP≌△BAP(SAS),
∴∠ADP=∠ABP,
在△CBP和△ABP中,
|
∴△CBP≌△ABP(SSS),
∴∠CBP=∠ABP,
∵∠ABC=60°,∠ADP=∠ABP,
∴∠ADP=∠ABP=30°.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定的应用,解此题的关键是推出∠CBP=∠ABP,∠ADP=∠ABP.

练习册系列答案
相关题目
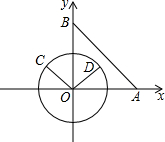 如图,在平面直角坐标系xOy中,点A(4,0),点B(0,4),动点C在以半径为2的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),当AC与⊙O相切时,点D的坐标为
如图,在平面直角坐标系xOy中,点A(4,0),点B(0,4),动点C在以半径为2的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),当AC与⊙O相切时,点D的坐标为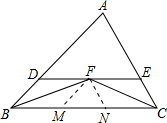 如图,∠ABC、∠ACB的平分线相交于点F.
如图,∠ABC、∠ACB的平分线相交于点F. 矩形ABCD沿对角线BD翻折BCD为BC′D,设C′B与AD交点为E,△BED面积为整个矩形面积的
矩形ABCD沿对角线BD翻折BCD为BC′D,设C′B与AD交点为E,△BED面积为整个矩形面积的
 如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=
如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=