题目内容
 矩形ABCD沿对角线BD翻折BCD为BC′D,设C′B与AD交点为E,△BED面积为整个矩形面积的
矩形ABCD沿对角线BD翻折BCD为BC′D,设C′B与AD交点为E,△BED面积为整个矩形面积的| 1 |
| 3 |
考点:翻折变换(折叠问题)
专题:
分析:首先根据题意结合图形求出线段DE与AD的数量关系,进而求出∠ABE的度数问题即可解决.
解答: 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,
∴AB⊥AD;
∴S△BED=
DE•AB,S四边形ABCD=AD•AB;
∵△BED面积为整个矩形面积的
,
∴
=
;
设DE=2k,则AD=3k,AE=k;
由题意得:∠EBD=∠CBD;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE=2k;
∴
=
=
,
∴∠ABE=30°,∠EBC=60°,
∴∠DBC=30°.
 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,∴AB⊥AD;
∴S△BED=
| 1 |
| 2 |
∵△BED面积为整个矩形面积的
| 1 |
| 3 |
∴
| DE |
| AD |
| 2 |
| 3 |
设DE=2k,则AD=3k,AE=k;
由题意得:∠EBD=∠CBD;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE=2k;
∴
| AE |
| BE |
| k |
| 2k |
| 1 |
| 2 |
∴∠ABE=30°,∠EBC=60°,
∴∠DBC=30°.
点评:该命题以矩形为载体,以翻折变换为手段,综合考查了全等三角形的性质、矩形的性质等几何知识点;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
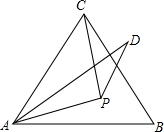 已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.
已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.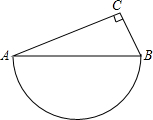 如图,在直角三角形ABC中,∠C=90°,AC=12,BC=5,则以AB为直径的半圆的面积为
如图,在直角三角形ABC中,∠C=90°,AC=12,BC=5,则以AB为直径的半圆的面积为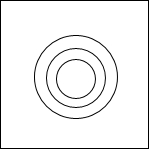 某健身俱乐部设置了如图所示的一个投镖靶,该靶是边长为18cm的正方形木板,镖靶从中心往外依次画有半径分别为1cm、2cm和3cm的同心圆,当投镖者投中最里层最小的圆时,获得一等奖;当投中小圆与中间圆围成的圆环时,可获得二等奖;当投中中圆与最大的圆围成的圆环时,可获得三等奖.若每人只投一镖,请你分别求出获得第一名和第三名的概率.(结果精确到0.01)
某健身俱乐部设置了如图所示的一个投镖靶,该靶是边长为18cm的正方形木板,镖靶从中心往外依次画有半径分别为1cm、2cm和3cm的同心圆,当投镖者投中最里层最小的圆时,获得一等奖;当投中小圆与中间圆围成的圆环时,可获得二等奖;当投中中圆与最大的圆围成的圆环时,可获得三等奖.若每人只投一镖,请你分别求出获得第一名和第三名的概率.(结果精确到0.01)