题目内容
19.(1)在同一直角坐标系中,画出函数y=-x2,y=-$\frac{1}{2}$x2,y=-2x2的图象,并考虑这些抛物线有什么共同点和不同点.(2)当a<0时,二次函数y=ax2的图象有什么特点?
分析 (1)利用描点法分别得出函数y=-x2,y=-$\frac{1}{2}$x2,y=-2x2的图象;
(2)利用所画图象得出二次函数y=ax2的图象性质.
解答  解:(1)如图所示:
解:(1)如图所示:
函数y=-x2,y=-$\frac{1}{2}$x2,y=-2x2的图象,共同点是顶点都在原点,开口方向向下,对称轴是y轴,
不同点是:开口的大小不同;
(2)由(1)可得:当a<0时,二次函数y=ax2的图象顶点都在原点,开口方向向下,对称轴是y轴.
点评 此题主要考查了二次函数的图象画法以及二次函数的性质,利用描点法画出函数图象是解题关键.

练习册系列答案
相关题目
7. 如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
 如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |
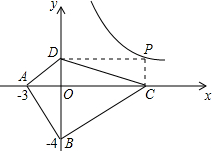 如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.
如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.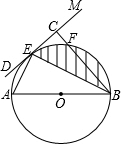 如图所示,已知⊙O的直径AB=8cm,BE为⊙O的弦,直接DM经过点E,且∠MEB=∠A作BC⊥DM于点C,BC交⊙O于点F,BC=6cm
如图所示,已知⊙O的直径AB=8cm,BE为⊙O的弦,直接DM经过点E,且∠MEB=∠A作BC⊥DM于点C,BC交⊙O于点F,BC=6cm