题目内容
19. 如图,在菱形ABCD中,AD=4,∠DAB=60°,P是AD的中点,M是对角线AC上的任意点,则PM+MD的最小值为2$\sqrt{3}$.
如图,在菱形ABCD中,AD=4,∠DAB=60°,P是AD的中点,M是对角线AC上的任意点,则PM+MD的最小值为2$\sqrt{3}$.
分析 找出D点关于AC的对称点B,连接PB交AC于M,此时MP+MD最小,且PB就是PM+MD的最小值,求出PB即可.
解答 解:连接PB交AC于M,连接DM,DB,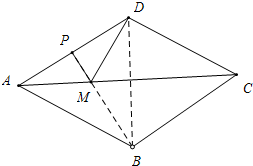 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴线段AC、BD互相垂直平分,
∴B、D关于AC对称,则MD=MB,
∴PM+MD=PM+BM=PB,
即PB就是PM+MD的最小值.
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∵AP=PD,
∴PB⊥AD(等腰三角形三线合一的性质).
在Rt△BDP中,BD=AD=4,PD=2
∴PB=$\sqrt{B{D}^{2}-P{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴PM+MD的最小值为2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题主要考查轴对称、最短路线问题、菱形的性质、垂直平分线的性质、勾股定理等知识点,确定点M的位置是解答本题的关键.

练习册系列答案
相关题目
10.分式方程$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$的根是( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
4.下列事件中,不可能事件是( )
| A. | 今年的除夕夜会下雪 | |
| B. | 在只装有红球的袋子里摸出一个黑球 | |
| C. | 射击运动员射击一次,命中10环 | |
| D. | 任意掷一枚硬币,正面朝上 |
8.下列事件中,为必然事件是( )
| A. | 度量三角形的内角和,结果是360° | |
| B. | 从仅装有5个黑球的口袋中摸出一球是黑球 | |
| C. | 购买中奖率为1%的100张彩票,结果中奖 | |
| D. | 汽车累积行驶1万千米,从未出现故障 |
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.