题目内容
15.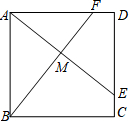 如图,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.求证:AE⊥BF.
如图,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.求证:AE⊥BF.
分析 首先证明△ABF≌△DAE(SAS),即可推出∠AFB=∠DEA,由∠D=90°,推出∠DEA+∠DAE=90°,推出∠AFB+∠DAE=90°,推出∠AMF=180°-90°=90°.
解答 证明:∵四边形ABCD是正方形,
∴∠BAD=∠ADE=90°,AD=AB=DC,
∵DF=CE,
∴AF=DE,
∵在△ABF和△DAE中,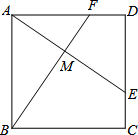
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠D}\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DAE(SAS);
∴∠AFB=∠DEA,
∵∠D=90°,
∴∠DEA+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AMF=180°-90°=90°,
∴AE⊥BF.
点评 本题考查了三角形的内角和定理,垂直定义,正方形性质,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
4.已知:x=$\sqrt{2+\sqrt{3}}$,y=$\sqrt{2-\sqrt{3}}$,则代数式x+y的值为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{2}$ |
5.下列说法错误的是( )
| A. | $\sqrt{3}$是3的平方根 | B. | |$\sqrt{2}$-1|=$\sqrt{2}$-1 | ||
| C. | -$\sqrt{5}$的相反数是$\sqrt{5}$ | D. | 带根号的数都是无理数 |
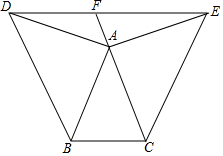 如图,△ABC中,AB=AC,∠BAC=40°,分别以AB、AC为边在形外作两个等腰直角三角形ABD和等腰直角三角形ACE,使∠BAD=∠CAE=90°.连结DE,CA的延长线交DE于F.
如图,△ABC中,AB=AC,∠BAC=40°,分别以AB、AC为边在形外作两个等腰直角三角形ABD和等腰直角三角形ACE,使∠BAD=∠CAE=90°.连结DE,CA的延长线交DE于F. 如图,在△ABC中,∠B=75°,∠C=45°,BC=6-2$\sqrt{3}$.求AB的长.
如图,在△ABC中,∠B=75°,∠C=45°,BC=6-2$\sqrt{3}$.求AB的长.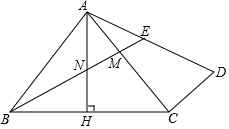 如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.