题目内容
在半径为5的⊙O中，弦AB长为8，P为弦AB上的一点，则OP长的整数值是 ．
考点：垂径定理,勾股定理
专题：
分析：根据题意画出图形，由图可知当OP垂直于AB是最短，当P与B重合时最长，求出OP的长即可．
解答：
解：如图所示，
∵AB=8，OP⊥AB，
∴BP=
AB=4．
∵OB=5，
∴OP=
=
=3，
∴3≤OP≤5，
∴OP长的整数值是3或4或5．
故答案为：3或4或5．
解：如图所示，∵AB=8，OP⊥AB，
∴BP=
| 1 |
| 2 |
∵OB=5，
∴OP=
| OB2-BP2 |
| 52-42 |
∴3≤OP≤5，
∴OP长的整数值是3或4或5．
故答案为：3或4或5．
点评：本题考查的是垂径定理，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
相关题目
已知点M（-2，3）在双曲线y=
上，则下列各点一定在该双曲线上的是（ ）
| k |
| x |
| A、（3，-2） |
| B、（-2，-3） |
| C、（2，3） |
| D、（3，2） |
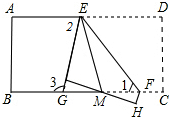把一张长方形纸片ABCD沿EF折叠，点B、C分别落在G、H的位置上，GH与CD相交于点M，EG的延长线与CD相交于点N，若∠1=55°，求∠2、∠3的度数．下列因式分解正确的是（ ）
| A、x2-xy+x=x（x-y） |
| B、a3-2a2b+ab2=a（a-b）2 |
| C、x2-2x+4=x（x-2）+4 |
| D、ax2-9=a（x+3）（x-3） |
用一个长60米的篱笆围成一个长方形鸡场（鸡场的一边靠墙，墙长为20米），如图，若BC=2AB，求AB和BC的长，并检验是否符合要求；若不符合要求，提出改进意见，并求出改进后的AB、BC的长，仍满足（BC=2AB）．