题目内容
 如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠FDE=α,则∠A=
如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠FDE=α,则∠A=考点:全等三角形的判定与性质
专题:计算题
分析:利用SAS得到三角形BDF与三角形CED全等,利用全等三角形对应角相等得到∠BFD=∠CDE,利用三角形内角和定理及等式的性质得到关于α的关系式,即可表示出∠A.
解答:解:在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴∠EDF=180°-∠CDE-∠BDF=180°-∠BFD-∠BDF=∠B,
∵∠B=
(180-∠A)=90°-
∠A,
∴∠EDF=α=90°-
∠A,
则∠A=180°-2α.
故答案为:180°-2α
|
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴∠EDF=180°-∠CDE-∠BDF=180°-∠BFD-∠BDF=∠B,
∵∠B=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDF=α=90°-
| 1 |
| 2 |
则∠A=180°-2α.
故答案为:180°-2α
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
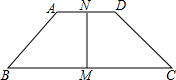 如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长.
如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长. 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.