题目内容
已知抛物线的顶点为C(1,5),与x轴相交于A、B,且△ABC的面积为15,求该抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:
分析:因抛物线过A(x1,0),B(x2,0)(x1<x2),且抛物线顶点顶点为C(1,5),所以A和B关于抛物线对称轴对称,于是
=1①;又因为△ABC的面积可表示为
×5=15②,将①②组成方程组,即可解出点A和点B的坐标和抛物线的解析式.
| x1+x2 |
| 2 |
| x2-x1 |
| 2 |
解答:解:∵抛物线过A(x1,0),B(x2,0)(x1<x2),且抛物线顶点顶点为C(1,5),
∴
=1①;
∵△ABC的面积为15,
∴
×5=15②,
组成方程组得
,
解得
,
∴A(-2,0),B(4,0),
∴
,
解得
,
∴函数解析式为y=-
x2+
x+
.
∴
| x1+x2 |
| 2 |
∵△ABC的面积为15,
∴
| x2-x1 |
| 2 |
组成方程组得
|
解得
|
∴A(-2,0),B(4,0),
∴
|
解得
|
∴函数解析式为y=-
| 5 |
| 9 |
| 10 |
| 9 |
| 40 |
| 9 |
点评:本题考查了待定系数法求解析式,解答此题不仅要熟知二次函数图象的性质,更要熟知二次函数与x轴交点坐标与对称轴的关系.

练习册系列答案
相关题目
 如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠FDE=α,则∠A=
如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠FDE=α,则∠A=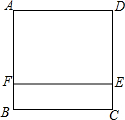 如图,从正方形ABCD上截取宽为2cm的矩形BCEF,剩下矩形AFED的面积为48cm2,则正方形ABCD的边长为
如图,从正方形ABCD上截取宽为2cm的矩形BCEF,剩下矩形AFED的面积为48cm2,则正方形ABCD的边长为