题目内容
5.代数式$\frac{1}{4}$a的值不小于$\frac{1}{2}$a+1的值,则a应满足( )| A. | a≤4 | B. | a≥4 | C. | a≤-4 | D. | a≥-4 |
分析 根据题意得出不等式,求出不等式的解集即可.
解答 解:根据题意得:$\frac{1}{4}$a≥$\frac{1}{2}$a+1,
解得:a≤-4,
故选C.
点评 本题考查了解一元一次不等式,能根据题意得出不等式是解此题的关键.

练习册系列答案
相关题目
10.能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (2x-y)(2y+x) | C. | (m-n)(n-m) | D. | 99×101 |
14. 先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
 先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )| A. | 10 | B. | 2$\sqrt{10}$ | C. | $\sqrt{61}$ | D. | $\sqrt{41}$ |
15.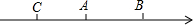 如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )
如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )
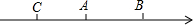 如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )
如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )| A. | -2-$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
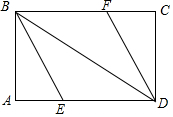 如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.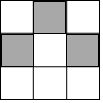 如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是$\frac{1}{3}$.
如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是$\frac{1}{3}$. 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是$\sqrt{10}$.
如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是$\sqrt{10}$.