��Ŀ����
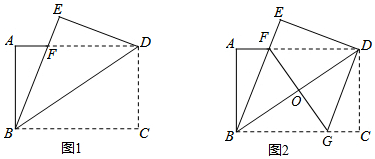
19����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2-2x-3��x����A��B���㣨��A�ڵ�B����ࣩ������������λ��x���Ϸ�������M������������λ��x���·�������x�ᷭ�ۣ����ۺ�����������N������N��y���ڵ�C������AC��BC����1��������N������������Ӧ�ĺ�������ʽ��
��2�����ABC���Բ�İ뾶��
��3����PΪ����M������N�ϵ�һ���㣬��QΪx���ϵ�һ�����㣬���Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ����Q�����꣮
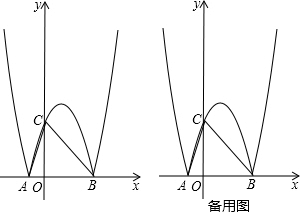
���� ��1������֪�����߿����A��B���꼰�������꣬���öԳ��Կ����C�����꣬���ô���ϵ�������������N�Ľ���ʽ��
��2�������Բ�Ķ����֪Բ�ļ�Ϊ�߶�BC��AB�Ĵ�ֱƽ���ߵĽ��㣬��ֱ��y=x�������߶Գ���Ľ��㣬��������Բ��Բ�ģ������ù��ɶ�������ð뾶�ij���
��3����Q��x��0������BCΪƽ���ı��εı�ʱ������BQ��PC��BQ=PC���Ӷ�����x��ʾ��P������꣬���������߽���ʽ�ɵõ�x�ķ��̣������Q�����꣬��BCΪƽ���ı��εĶԽ���ʱ����B��C����������ƽ���ı��εĶԳ����ĵ����꣬�Ӷ��ɱ�ʾ��P�����꣬���������߽���ʽ�ɵõ�����x�ķ��̣������P�����꣮
��� �⣺
��1����y=x2-2x-3�У���y=0�ɵ�x2-2x-3=0�����x=-1��x=3��
��A��-1��0����B��3��0����
��x=0�ɵ�y=-3��
��������λ��x���·�������x�ᷭ�ۺ�õ�����N��
��C��0��3����
������N�Ľ���ʽΪy=ax2+bx+c��
��A��B��C���������ɵ�$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$��
������N������������Ӧ�ĺ�������ʽΪy=-x2+2x+3��
��2�����ABC���Բ��Բ��ΪM�����MΪ�߶�BC���߶�AB��ֱƽ���ߵĽ��㣬
��B��3��0����C��0��3����
���߶�BC�Ĵ�ֱƽ���ߵĽ���ʽΪy=x��
���߶�AB�Ľ���ʽΪ����N�ĶԳ��ᣬ��x=1��
��M��1��1����
��MB=$\sqrt{��1-3��^{2}+{1}^{2}}$=$\sqrt{5}$��
����ABC���Բ�İ뾶Ϊ$\sqrt{5}$��
��3����Q��t��0������BQ=|t-3|
�ٵ�BCΪƽ���ı��εı�ʱ����ͼ1������BQ��PC��
��P��������Ϊ3��
����C����x��ƽ�е�ֱ��������M������N�Ľ��㼴Ϊ��P��x���϶�Ӧ�ļ�Ϊ��Q��
����P������M��ʱ����y=x2-2x-3�У���y=3�ɽ��x=1+$\sqrt{7}$��x=1-$\sqrt{7}$��
��PC=1+$\sqrt{7}$��PC=$\sqrt{7}$-1��
��x=1+$\sqrt{7}$ʱ����֪��Q�ڵ�B���Ҳ࣬�ɵ�BQ=t-3��
��t-3=1+$\sqrt{7}$�����t=4+$\sqrt{7}$��
��x=1-$\sqrt{7}$ʱ����֪��Q�ڵ�B����࣬�ɵ�BQ=3-t��
��3-t=$\sqrt{7}$-1�����t=4-$\sqrt{7}$��
��Q��������4+$\sqrt{7}$��0����4-$\sqrt{7}$��0����
����P������N��ʱ����y=-x2+2x+3�У���y=3�����x=0����ȥ����x=2��
��PC=2��
��ʱQ����B����Ҳ࣬��BQ=t-3��
��t-3=2�����t=5��
��Q��������5��0����
�ڵ�BCΪƽ���ı��εĶԽ���ʱ��
��B��3��0����C��0��3����
���߶�BC���е�Ϊ��$\frac{3}{2}$��$\frac{3}{2}$������P��x��y����
��x+t=3��y+0=3�����x=3-t��y=3��
��P��3-t��3����
����P������M��ʱ������3=��3-t��2-2��3-t��-3�����t=2+$\sqrt{7}$��t=2-$\sqrt{7}$��
��Q��������2+$\sqrt{7}$��0����2-$\sqrt{7}$��0����
����P������N��ʱ������3=-��3-t��2+2��3-t��+3�����t=3��Q��B�غϣ���ȥ����t=1��
��Q��������1��0����
���Ͽ�֪Q�������Ϊ��4+$\sqrt{7}$��0����4-$\sqrt{7}$��0����5��0����2+$\sqrt{7}$��0����2-$\sqrt{7}$��0����1��0����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ�������ԳƵ����ʡ����������ġ����ɶ�����ƽ���ı��ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1����ȷ������������ǽ���Ĺؼ����ڣ�2����ȷ�������ĵ�λ�ú������ǽ���Ĺؼ����ڣ�3����ȷ����P���λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ر����һ�ʣ�����ܶ࣬�ѶȽϴ�

 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�| A�� | a��4 | B�� | a��4 | C�� | a��-4 | D�� | a��-4 |
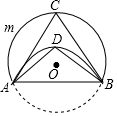 ��ͼ������O����AB�۵�����C��$\widehat{AmB}$�ϣ���D��$\widehat{AB}$�ϣ�����ACB=70�㣬���ADB=110�㣮
��ͼ������O����AB�۵�����C��$\widehat{AmB}$�ϣ���D��$\widehat{AB}$�ϣ�����ACB=70�㣬���ADB=110�㣮