题目内容
11.请你设计实验方案,估计任意6个人有2个人是同一个月生日的概率.分析 首先看出至少有两个人的生日是同一个月的对立事件,对立事件是六个人中没有人的生日在同一个月,这是一个等可能事件的概率,试验发生包含的事件数126,满足条件的事件是6个人生日分别在六个月,共有A126种结果,根据古典概型概率公式得到结果.
解答 解:设至少有两个人的生日是同一个月为事件A,
则$\overline{A}$表示六个人中没有人的生日在同一个月,
P($\overline{A}$)=$\frac{{A}_{12}^{6}}{1{2}^{6}}=0.02984\$,
根据对立事件的概率得到P(A)=1-0.02984=0.77720.
点评 本题是一个生日问题,考查对立事件的概率,对立事件是指同一次试验中,不会同时发生的事件,遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,在△ABC中,∠CAB=90°,将△ABC绕点A顺时针旋转60°得△ADE,则∠EAB的度数为( )
如图,在△ABC中,∠CAB=90°,将△ABC绕点A顺时针旋转60°得△ADE,则∠EAB的度数为( )
 如图,在△ABC中,∠CAB=90°,将△ABC绕点A顺时针旋转60°得△ADE,则∠EAB的度数为( )
如图,在△ABC中,∠CAB=90°,将△ABC绕点A顺时针旋转60°得△ADE,则∠EAB的度数为( )| A. | 20° | B. | 25° | C. | 28° | D. | 30° |
16.下列各式从左到右的变形,属于因式分解的是( )
| A. | a2-b2=(a-b)(a+b) | B. | mx+my+nx+ny=m(x+y)+n(x+y) | ||
| C. | (x+1)(x-1)=x2-1 | D. | x2-2x+1=x(x-2)+1 |
 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC.
如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为4,则这个反比例函数的解析式为y=-$\frac{4}{x}$.
如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为4,则这个反比例函数的解析式为y=-$\frac{4}{x}$.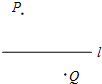 已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.
已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.