题目内容
3.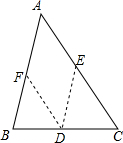 已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.
已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.解:在边BC上任意选取一点D,作DE∥AB,交AC于E,作DF∥AC,交AB于F.
因为DE∥AB
所以∠EDC=∠B,∠DEC=∠A.
分析 由题目思路可知是把∠A、∠B、∠C转化在点D处,再利用平角的定义可得到结论.
解答 解:在边BC上任意选取一点D,作DE∥AB,交AC于E,作DF∥AC,交AB于F.
因为DE∥AB
所以∠EDC=∠B,∠DEC=∠A.
因为DF∥AC,
所以∠BDF=∠C,∠EDF=∠DEC=∠A,
∵∠EDF+∠EDC+∠BDF=180°,
∴∠A+∠B+∠C=180°.
点评 本题主要考查三角形内角和定理的证明,把三个角转化到同一顶点处,构成一个平角是证明的基本思路.

练习册系列答案
相关题目
11. 如图,若∠1=100°,∠C=70°,则∠A的度数为( )
如图,若∠1=100°,∠C=70°,则∠A的度数为( )
 如图,若∠1=100°,∠C=70°,则∠A的度数为( )
如图,若∠1=100°,∠C=70°,则∠A的度数为( )| A. | 20° | B. | 30° | C. | 70° | D. | 80° |
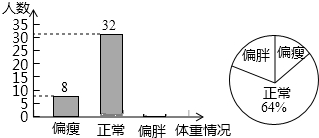

 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=6cm,则EF=6cm.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=6cm,则EF=6cm.