题目内容
14.(1)比较a2+b2与2ab的大小(用“>”、“<”或“=”填空):①当a=3,b=2时,a2+b2>2ab,
②当a=-1,b=-1时,a2+b2=2ab,
③当a=1,b=-2是,a2+b2>2ab.
(2)猜想a2+b2与2ab有怎样的大小关系?并证明你的结论.
分析 (1)①代入a,b的值,分别计算出a2+b2、2ab,即可解答;
②代入a,b的值,分别计算出a2+b2、2ab,即可解答;
③代入a,b的值,分别计算出a2+b2、2ab,即可解答;
(2)将作差,即可比较大小.
解答 解:(1)①当a=3,b=2时,a2+b2=13,2ab=12,
∴a2+b2>2ab;
②当a=-1,b=-1时,a2+b2=2,2ab=2,
∴a2+b2=2ab;
③当a=1,b=2时,a2+b2=5,2ab=4,
∴a2+b2>2ab;
故答案为:①>,②=,③>;
(2)∵a2+b2-2ab=(a-b)2≥0,
∴a2+b2≥2ab.
点评 本题考查了完全平分公式,解决本题的关键是熟记完全平分公式.

练习册系列答案
相关题目
4.样本数据2,3,a,5,1的平均数是3,则这个样本的方差是( )
| A. | 4.5 | B. | 3 | C. | 2 | D. | $\sqrt{5}$ |
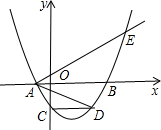 如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.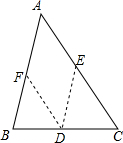 已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.
已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.