题目内容
11.定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)×(3-4i)=5-3i.
(1)填空:i3=-i,i4=1;
(2)计算①(3+i)(3-i);②(5-2i)2;
(3)若两个复数相等,则它们的实部和虚部必须完全相等,完成下列问题:已知:(x+y)-3i=(1-x)+yi,(x,y为实数),求x,y的值;
(4)试一试:请将$\frac{2-i}{2+i}$化简成a+bi的形式.
分析 (1)把i2=-1代入求出即可;
(2)①先根据平方差公式进行计算,再把i2=-1代入求出即可;
②先根据完全平方公式进行计算,再把i2=-1代入求出即可;
(3)根据两个复数相等的定义得出方程组,求出方程组的解即可;
(4)根据分子和分母都乘以2-i,再进行计算即可.
解答 解:(1)i3=i2•i=-i,i4=(i2)2=(-1)2=1,
故答案为:-i,1;
(2)①(3+i)(3-i)
=9-i2
=9-(-1)
=10;
②(5-2i)2
=25-20i+4i2
=25-20i+4×(-1)
=21-20i;
(3)(x+y)-3i=(1-x)+yi,
∴$\left\{\begin{array}{l}{x+y=1-x}\\{y=-3}\end{array}\right.$
解得:x=2,y=-3;
(4)$\frac{2-i}{2+i}$
=$\frac{(2-i)^{2}}{(2+i)(2-i)}$
=$\frac{4-4i+{i}^{2}}{4-{i}^{2}}$
=$\frac{4-4i+(-1)}{4-(-1)}$
=$\frac{5-4i}{5}$
=1-0.8i.
点评 本题考查了复数,整式的混合运算的应用,能读懂题意是解此题的关键,主要考查了学生的理解能力和计算能力,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.方程2x2+3x+2=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个实数根 | D. | 沒有实数根 |
16.一元二次方程x2+4x+4=0的根是( )
| A. | x1=4,x2=-4 | B. | x1=x2=-2 | C. | x1=2,x2=-2 | D. | x1=0,x2=-2 |
20.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
| A. | 11+$\frac{11\sqrt{3}}{2}$ | B. | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C. | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D. | 11-$\frac{11\sqrt{3}}{2}$ |
1.在$\sqrt{3}$,-1,0,-$\sqrt{2}$这四个数中,最大的是( )
| A. | $\sqrt{3}$ | B. | 0 | C. | -1 | D. | -$\sqrt{2}$ |
 如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.
如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.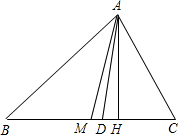 如图,AD,AM,AH分别△ABC的角平分线、中线和高,请结合图形,写出三个不同的相等关系式AH<AB、AH<AD、AH<AM.
如图,AD,AM,AH分别△ABC的角平分线、中线和高,请结合图形,写出三个不同的相等关系式AH<AB、AH<AD、AH<AM.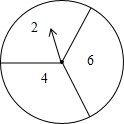 把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.
把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.