题目内容
14.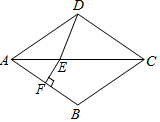 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,连接DE,则∠CDE=60°.
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,连接DE,则∠CDE=60°.
分析 连接BE,根据菱形的对角线平分一组对角线可得∠BAC=40°,根据线段垂直平分线上的点到两端点的距离相等可得AE=BE,根据等边对等角可得∠ABE=∠BAC,再根据菱形的邻角互补求出∠ABC,然后求出∠CBE,最后根据菱形的对称性可得∠CDE=∠CBE.
解答 解:如图,连接BE,
在菱形ABCD中,∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×80°=40°,
∵EF是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠BAC=40°,
∵菱形ABCD的对边AD∥BC,
∴∠ABC=180°-∠BAD=180°-80°=100°,
∴∠CBE=∠ABC-∠ABE=100°-40°=60°,
由菱形的对称性,∠CDE=∠CBE=60°.
故答案为60°.
点评 本题考查了菱形的性质,线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,熟记各性质是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4.下列不等式中一定成立的是( )
| A. | 5a>4a | B. | -a>-2a | C. | a+2<a+3 | D. | $\frac{2}{a}$<$\frac{3}{a}$ |
 尺规作图(不写作法,保留作图痕迹,写明结论):在数轴上作出表示-$\sqrt{17}$的点.
尺规作图(不写作法,保留作图痕迹,写明结论):在数轴上作出表示-$\sqrt{17}$的点.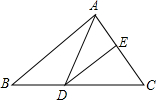 如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.
如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm. 如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°.
如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°.